【動画を差し替えました。】3D化した数式をblenderを使って回転させる。

はじめに

ちょっと前になってしまいましたが、数式を3D化する方法について書きました。本記事では、これをBlender(2.78a)で回転させてみることにします。

3D化した数式をファイルから読み込む。

3D化した数式は以下の手順で読み込むことができます。

Blenderを起動します。
メニューバーの「ファイル」→「開く」を選択します。
ファイルブラウザーが開くので、3D化した数式に対応したファイルをクリックし、「Blenderファイルを開く」ボタンを押します。
3Dビューに数式が表示されます。

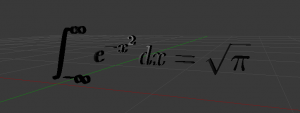
いざ、回転。

読み込んだ数式は以下の手順で回転させることができます。

何フレームで1回転させるかを決めます。ここでは\(n\)フレーム進むと\(z\)軸の周りを反時計回りに1回転すると仮定します。なおフレームレートを\(f\)とすると、1回転に必要な時間(秒)は\(n/f\)となります(\(f=29.97\)の場合には、\(f=30\)とみなしても(たぶん)良いと思います)。
オブジェクトモードに切り替えて、回転させたい立体を選択します。
ツールシェルフのツールタブから「原点を設定」→「原点を重心へ移動」を選択します。すると、3Dカーソルが立体(群)の重心の位置に移動します。
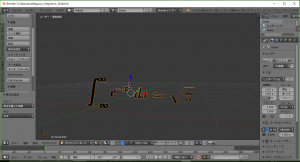
タイムラインビューで回転を開始させたいフレーム番号を選択します。以下の画像ではフレーム番号”1″を選択しています。
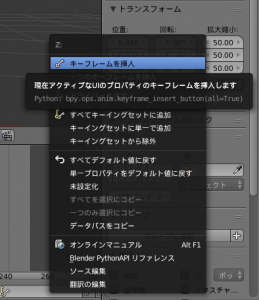
プロパティシェルフの回転の”Z:”のところで右クリックします。

するとメニューが表示されますので、「キーフレームを挿入」を選択し、キーフレームを挿入します。
タイムラインビューで手順4で指定したフレーム番号に\(n-1\)を加算した数に相当するフレーム番号を選択します。以下の画像ではフレーム番号”15″を選択しています。すなわち\(n=15\)としていることになります。
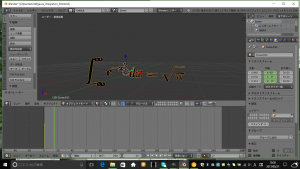
プロパティシェルフの回転の”Z:”を左クリックし、\(360\cdot\displaystyle {\frac {n-1}{n}}\)に相当する数を入力し、Enterキーで入力を確定させます。以下の画像では\(360\cdot\displaystyle{\frac{14}{15}} = 336\)を入力しています。
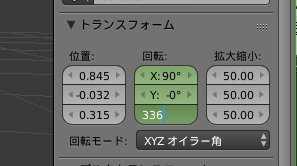
プロパティシェルフの回転の”Z:”のところで右クリックします。するとメニューが表示されますので、「キーフレームを挿入」を選択し、キーフレームを挿入します。
タイムラインビューで手順6で指定したフレーム番号の次のフレーム番号(\(n+1\))を指定します。
プロパティシェルフの回転の”Z:”を左クリックして0を入力し、Enterキーで入力を確定させます。
プロパティシェルフの回転の”Z:”のところで右クリックする。するとメニューが表示されますので、「キーフレームを挿入」を選択し、キーフレームを挿入します。
このままだと、\(z\)軸周りに回転するように設定はできているものの、一定の角速度で回転してくれませんので、一定の角速度で回転させるように設定を行います。まず、「グラフエディタ」を選択します。
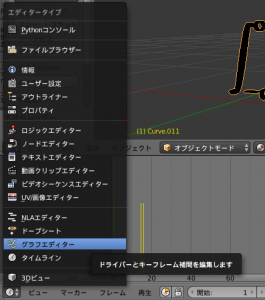
「Zオイラー角回転」を左クリックし、選択状態とします。
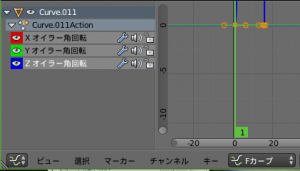
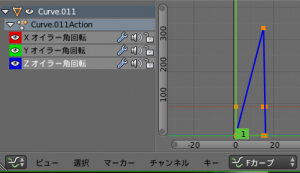
グラフの表示範囲が適切でない場合には、前の手順でクリックしたところの脇にある縦方向のスクロールバーで表示範囲を調整します。うまく調整できると、下図のような表示になるのですが、グラフが直線的な感じになっていなさそうなことがわかります。
下部のメニューバーから「キー」→「補間モード」→「リニア」と選択します。

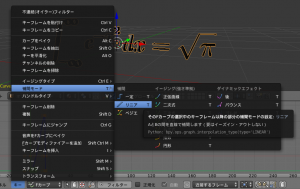
すると、(ちょっとわかりにくいかもしれませんが、)下図のようにグラフが折れ線に変化することがわかります。
ここまでの操作で数式を1回転させることができます。矢印キーのうち[◀]または[▶]を押すと1フレームごとに後退または前進させることができます。またレンダリングはそれなりに時間がかかりますので、動画を作成する前にどんな感じになるのか下の動画のような感じで確認するとよいかもしれません。
[2017/10/05補足] 動画を差し替えました。