はじめに
前の記事で、Eclipseのワークベンチ上でできるだけ簡単にScalaのプロジェクトを作成する方法について書きました。
この記事ではそれに引き続き、複素数を扱うためのコードをScalaで書いてみます… と思ってちょっとググってみると、Breezeに複素数を扱うためのクラス等があるようですので、そいつの一部を写経しながら複素数を扱うためのコードを書いてみることにします。
スポンサーリンク
コードを書くための準備。
コードを書く前に、以下の手順でScalaプロジェクトにコードを格納するためのパッケージ及びコードを記述するためのファイルを作成します。
- Scalaプロジェクトのsource folderを右クリックします。すると、ポップアップメニューが表示されますので、「New」→「Package」を選択します(下図)。
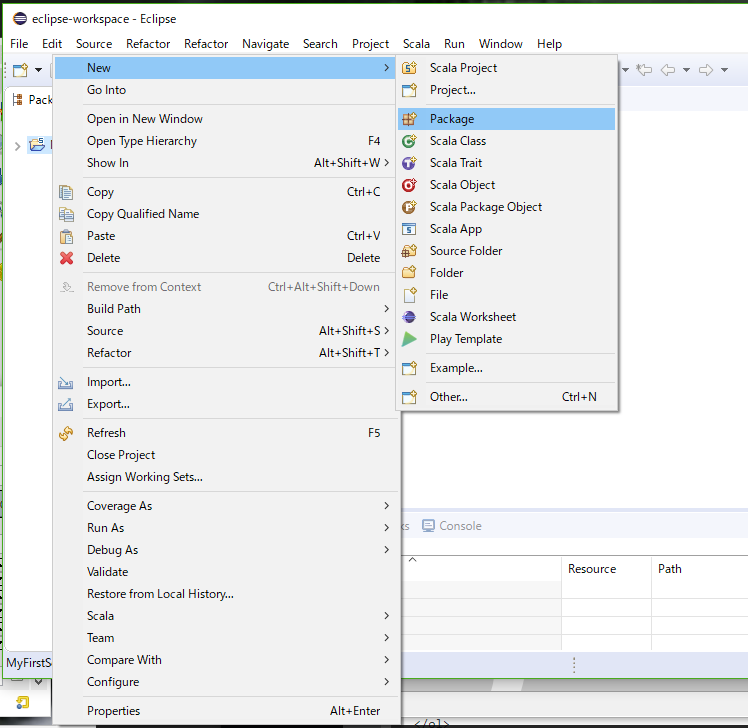
- 「package」ウィザードが表示されますので、「Name:」フィールド(下図の(a))にパッケージ名を入力します。ここではパッケージ名は”info.pandanote.test”としておきます。
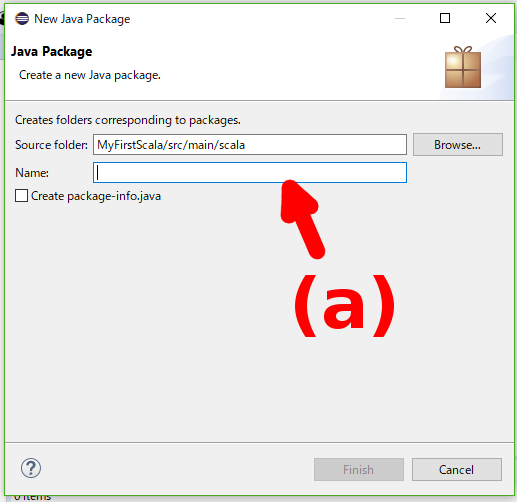
パッケージ名を入力すると「Finish」ボタンが押せるようになりますので、「Finish」ボタンを押します。 - 「package」ウィザードが消え、Scalaプロジェクトに手順2で入力した名前のパッケージが作成されます(下図)。
- 手順3で作成したパッケージをPackage Explorer上で右クリックするとポップアップメニューが表示されますので、「New」→「Scala class」と選択します(下図)。
- 「New File」ウィザードが表示されますので、「Name:」フィールドにすでに指定されているパッケージ名の後ろに「ComplexNumber」と書き足し(下図の(a))、「Finish」ボタンを押します。
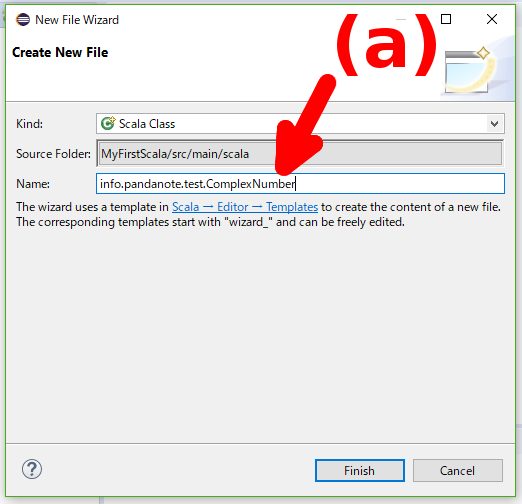
- ComplexNumber.scalaという名前のファイルが作成されます(下図の(a))。なお、生成されたファイルにはComplexNumberクラスのスケルトンが記述されています(下図の(b))。
プログラムを記述します。
プログラムのリスト
ファイルを作成したら、プログラムを記述します。Breezeで実装されているComplexクラスを参考にして、以下のようなオブジェクト(ComplexNumberオブジェクト)及びクラス(ComplexNumberクラス)を書いてみました。
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| package info.pandanote.test | |
| import scala.reflect.ClassTag | |
| import scala.math._ | |
| package info.pandanote.test | |
| import scala.reflect.ClassTag | |
| import scala.math._ | |
| // BreezeのComplexクラスを元にして複素数を扱うためのクラスを書いてみました。 | |
| // 電気工学的な虚数単位が設定できるようにコンストラクタの引数を変更しています。 | |
| case class ComplexNumber(real: Double, imag: Double = 0.0, imagUnit: String = "i") { | |
| // 虚数成分の符号を考慮して、少し見やすくしてみました。 | |
| override def toString(): String = real + (if (imag==0.0) "" else ((if (imag>0.0)"+"else"-") + (if (imag>0.0)imag else -imag) + imagUnit)) | |
| def re() = real | |
| def im() = imag | |
| def +(that: ComplexNumber) = ComplexNumber(this.real+that.real,this.imag+that.imag,this.imagUnit) | |
| def +(that: Int) = ComplexNumber(this.real+that,this.imag,this.imagUnit) | |
| def +(that: Long) = ComplexNumber(this.real+that,this.imag,this.imagUnit) | |
| def +(that: Float) = ComplexNumber(this.real+that,this.imag,this.imagUnit) | |
| def +(that: Double) = ComplexNumber(this.real+that,this.imag,this.imagUnit) | |
| def -(that: ComplexNumber) = ComplexNumber(this.real-that.real,this.imag-that.imag,this.imagUnit) | |
| def -(that: Int) = ComplexNumber(this.real-that,this.imag,this.imagUnit) | |
| def -(that: Long) = ComplexNumber(this.real-that,this.imag,this.imagUnit) | |
| def -(that: Float) = ComplexNumber(this.real-that,this.imag,this.imagUnit) | |
| def -(that: Double) = ComplexNumber(this.real-that,this.imag,this.imagUnit) | |
| def *(that: ComplexNumber) = ComplexNumber(this.real*that.real - this.imag*that.imag, this.real*that.imag+this.imag*that.real,this.imagUnit) | |
| def *(that: Int) = ComplexNumber(this.real*that,this.imag*that,this.imagUnit) | |
| def *(that: Long) = ComplexNumber(this.real*that,this.imag*that,this.imagUnit) | |
| def *(that: Float) = ComplexNumber(this.real*that,this.imag*that,this.imagUnit) | |
| def *(that: Double) = ComplexNumber(this.real*that,this.imag*that,this.imagUnit) | |
| def /(that: ComplexNumber) = { | |
| val xnorm = that.real*that.real+that.imag*that.imag | |
| ComplexNumber((this.real*that.real+this.imag*that.imag)/xnorm,(this.imag*that.real-this.real*that.imag)/xnorm,this.imagUnit) | |
| } | |
| def /(that: Int) = ComplexNumber(this.real/that,this.imag/that,this.imagUnit) | |
| def /(that: Long) = ComplexNumber(this.real/that,this.imag/that,this.imagUnit) | |
| def /(that: Float) = ComplexNumber(this.real/that,this.imag/that,this.imagUnit) | |
| def /(that: Double) = ComplexNumber(this.real/that,this.imag/that,this.imagUnit) | |
| // 複素数の剰余計算というものが定義されているのかどうかわかりませんが、書いてみました。 | |
| // この部分はBreezeの実装とは異なります。 | |
| def %(that: ComplexNumber) = { | |
| val div = this./(that) | |
| this - ComplexNumber(Math.round(div.re()),Math.round(div.im()),this.imagUnit)*that | |
| } | |
| def %(that: Int): ComplexNumber = this.%(ComplexNumber(that, 0, this.imagUnit)) | |
| def %(that: Long): ComplexNumber = %(ComplexNumber(that, 0, this.imagUnit)) | |
| def %(that: Float): ComplexNumber = %(ComplexNumber(that, 0, this.imagUnit)) | |
| def %(that: Double): ComplexNumber = %(ComplexNumber(that, 0, this.imagUnit)) | |
| def unary_- = ComplexNumber(-real,-imag,this.imagUnit) | |
| def abs = math.sqrt(real*real+imag*imag) | |
| def conjugate = ComplexNumber(real,-imag,this.imagUnit) | |
| def log = ComplexNumber(math.log(abs),math.atan2(imag,real),this.imagUnit) | |
| def exp = { | |
| val expreal = math.exp(real) | |
| ComplexNumber(expreal*math.cos(imag),expreal*math.sin(imag),this.imagUnit) | |
| } | |
| def pow(that: Int): ComplexNumber = pow(ComplexNumber(that,0,this.imagUnit)) | |
| def pow(that: Double): ComplexNumber = pow(ComplexNumber(that,0,this.imagUnit)) | |
| def pow(that: ComplexNumber): ComplexNumber = { | |
| if (that == ComplexNumber.zero) ComplexNumber.one | |
| else if (this == ComplexNumber.zero) { | |
| if (that.imag != 0.0 || that.real < 0.0) ComplexNumber.nan | |
| else ComplexNumber.zero | |
| } else { | |
| val c = log * that | |
| val expReal = math.exp(c.real) | |
| ComplexNumber(expReal*math.cos(c.imag),expReal*math.sin(c.imag),this.imagUnit) | |
| } | |
| } | |
| // こんなのも定義してみます。 | |
| def **(that: ComplexNumber): ComplexNumber = pow(that) | |
| def **(that: Double): ComplexNumber = pow(that) | |
| def **(that: Int): ComplexNumber = pow(that) | |
| override def equals(that: Any) = that match { | |
| case that: ComplexNumber => this.real == that.real && this.imag == that.imag | |
| case real: Double => this.real == real && this.imag == 0 | |
| case real: Int => this.real == real && this.imag == 0 | |
| case real: Short => this.real == real && this.imag == 0 | |
| case real: Long => this.real == real && this.imag == 0 | |
| case real: Float => this.real == real && this.imag == 0 | |
| case _ => false | |
| } | |
| def >(that: ComplexNumber) = | |
| (this.real > that.real || (this.real == that.real && this.imag > that.imag)) | |
| def >=(that: ComplexNumber) = | |
| (this.real >= that.real || (this.real == that.real && this.imag >= that.imag)) | |
| def <(that: ComplexNumber) = | |
| (this.real < that.real || (this.real == that.real && this.imag < that.imag)) | |
| def <=(that: ComplexNumber) = | |
| (this.real <= that.real || (this.real == that.real && this.imag <= that.imag)) | |
| // 試しにこんな演算子を定義してみます。 | |
| def <>(that: ComplexNumber) = | |
| (this.real != that.real || this.imag != that.imag) | |
| override def hashCode() = real.## ^ imag.## | |
| } | |
| object ComplexNumber { | |
| outer => | |
| val one = new ComplexNumber(1,0) | |
| val zero = new ComplexNumber(0,0) | |
| val imaginaryUnit = new ComplexNumber(0,1) | |
| val nan = new ComplexNumber(Double.NaN,Double.NaN) | |
| // Javaでいうところのstaticなメソッドみたいなものです。 | |
| def exp(that: ComplexNumber): ComplexNumber = that.exp | |
| def log(that: ComplexNumber): ComplexNumber = that.log | |
| // 実数に複素数を作用させる演算が定義されていなかったので、追加しました。 | |
| // 試行錯誤の末、以下の一行になりました… | |
| implicit def fromDouble(d: Double) = new ComplexNumber(d) | |
| } | |
| // BreezeのComplexクラスを元にして複素数を扱うためのクラスを書いてみました。 | |
| // jを虚数単位として設定できるようにコンストラクタの引数を変更しています。 | |
| // 詳細はこちら→ https://pandanote.info/?p=1829 | |
| case class ComplexNumber(real: Double, imag: Double, imagUnit: String = "i") { | |
| // 虚数成分の符号を考慮して、少し見やすくしてみました。 | |
| override def toString(): String = real + (if (imag==0.0) "" else ((if (imag>0.0)"+"else"-") + (if (imag>0.0)imag else -imag) + imagUnit)) | |
| def re() = real | |
| def im() = imag | |
| def +(that: ComplexNumber) = ComplexNumber(this.real+that.real,this.imag+that.imag,this.imagUnit) | |
| def +(that: Int) = ComplexNumber(this.real+that,this.imag,this.imagUnit) | |
| def +(that: Long) = ComplexNumber(this.real+that,this.imag,this.imagUnit) | |
| def +(that: Float) = ComplexNumber(this.real+that,this.imag,this.imagUnit) | |
| def +(that: Double) = ComplexNumber(this.real+that,this.imag,this.imagUnit) | |
| def -(that: ComplexNumber) = ComplexNumber(this.real-that.real,this.imag-that.imag,this.imagUnit) | |
| def -(that: Int) = ComplexNumber(this.real-that,this.imag,this.imagUnit) | |
| def -(that: Long) = ComplexNumber(this.real-that,this.imag,this.imagUnit) | |
| def -(that: Float) = ComplexNumber(this.real-that,this.imag,this.imagUnit) | |
| def -(that: Double) = ComplexNumber(this.real-that,this.imag,this.imagUnit) | |
| def *(that: ComplexNumber) = ComplexNumber(this.real*that.real - this.imag*that.imag, this.real*that.imag+this.imag*that.real,this.imagUnit) | |
| def *(that: Int) = ComplexNumber(this.real*that,this.imag*that,this.imagUnit) | |
| def *(that: Long) = ComplexNumber(this.real*that,this.imag*that,this.imagUnit) | |
| def *(that: Float) = ComplexNumber(this.real*that,this.imag*that,this.imagUnit) | |
| def *(that: Double) = ComplexNumber(this.real*that,this.imag*that,this.imagUnit) | |
| def /(that: ComplexNumber) = { | |
| val xnorm = that.real*that.real+that.imag*that.imag | |
| ComplexNumber((this.real*that.real+this.imag*that.imag)/xnorm,(this.imag*that.real-this.real*that.imag)/xnorm,this.imagUnit) | |
| } | |
| def /(that: Int) = ComplexNumber(this.real/that,this.imag/that,this.imagUnit) | |
| def /(that: Long) = ComplexNumber(this.real/that,this.imag/that,this.imagUnit) | |
| def /(that: Float) = ComplexNumber(this.real/that,this.imag/that,this.imagUnit) | |
| def /(that: Double) = ComplexNumber(this.real/that,this.imag/that,this.imagUnit) | |
| // 複素数の剰余計算というものが定義されているのかどうかわかりませんが、書いてみました。 | |
| // この部分はBreezeの実装とは異なります。 | |
| def %(that: ComplexNumber) = { | |
| val div = this./(that) | |
| this - ComplexNumber(Math.round(div.re()),Math.round(div.im()),this.imagUnit)*that | |
| } | |
| def %(that: Int): ComplexNumber = this.%(ComplexNumber(that, 0, this.imagUnit)) | |
| def %(that: Long): ComplexNumber = %(ComplexNumber(that, 0, this.imagUnit)) | |
| def %(that: Float): ComplexNumber = %(ComplexNumber(that, 0, this.imagUnit)) | |
| def %(that: Double): ComplexNumber = %(ComplexNumber(that, 0, this.imagUnit)) | |
| def unary_- = ComplexNumber(-real,-imag,this.imagUnit) | |
| def abs = math.sqrt(real*real+imag*imag) | |
| def conjugate = ComplexNumber(real,-imag,this.imagUnit) | |
| def log = ComplexNumber(math.log(abs),math.atan2(imag,real),this.imagUnit) | |
| def exp = { | |
| val expreal = math.exp(real) | |
| ComplexNumber(expreal*math.cos(imag),expreal*math.sin(imag),this.imagUnit) | |
| } | |
| def pow(that: Int): ComplexNumber = pow(ComplexNumber(that,0,this.imagUnit)) | |
| def pow(that: Double): ComplexNumber = pow(ComplexNumber(that,0,this.imagUnit)) | |
| def pow(that: ComplexNumber): ComplexNumber = { | |
| if (that == ComplexNumber.zero) ComplexNumber.one | |
| else if (this == ComplexNumber.zero) { | |
| if (that.imag != 0.0 || that.real < 0.0) ComplexNumber.nan | |
| else ComplexNumber.zero | |
| } else { | |
| val c = log * that | |
| val expReal = math.exp(c.real) | |
| ComplexNumber(expReal*math.cos(c.imag),expReal*math.sin(c.imag),this.imagUnit) | |
| } | |
| } | |
| // こんなのも定義してみます。 | |
| def **(that: ComplexNumber): ComplexNumber = pow(that) | |
| def **(that: Double): ComplexNumber = pow(that) | |
| def **(that: Int): ComplexNumber = pow(that) | |
| override def equals(that: Any) = that match { | |
| case that: ComplexNumber => this.real == that.real && this.imag == that.imag | |
| case real: Double => this.real == real && this.imag == 0 | |
| case real: Int => this.real == real && this.imag == 0 | |
| case real: Short => this.real == real && this.imag == 0 | |
| case real: Long => this.real == real && this.imag == 0 | |
| case real: Float => this.real == real && this.imag == 0 | |
| case _ => false | |
| } | |
| def >(that: ComplexNumber) = | |
| (this.real > that.real || (this.real == that.real && this.imag > that.imag)) | |
| def >=(that: ComplexNumber) = | |
| (this.real >= that.real || (this.real == that.real && this.imag >= that.imag)) | |
| def <(that: ComplexNumber) = | |
| (this.real < that.real || (this.real == that.real && this.imag < that.imag)) | |
| def <=(that: ComplexNumber) = | |
| (this.real <= that.real || (this.real == that.real && this.imag <= that.imag)) | |
| // 試しにこんな演算子を定義してみます。 | |
| def <>(that: ComplexNumber) = | |
| (this.real != that.real || this.imag != that.imag) | |
| override def hashCode() = real.## ^ imag.##package info.pandanote.test | |
| import scala.reflect.ClassTag | |
| import scala.math._ | |
| // BreezeのComplexクラスを元にして複素数を扱うためのクラスを書いてみました。 | |
| // 電気工学的な虚数単位が設定できるようにコンストラクタの引数を変更しています。 | |
| case class ComplexNumber(real: Double, imag: Double = 0.0, imagUnit: String = "i") { | |
| // 虚数成分の符号を考慮して、少し見やすくしてみました。 | |
| override def toString(): String = real + (if (imag==0.0) "" else ((if (imag>0.0)"+"else"-") + (if (imag>0.0)imag else -imag) + imagUnit)) | |
| def re() = real | |
| def im() = imag | |
| def +(that: ComplexNumber) = ComplexNumber(this.real+that.real,this.imag+that.imag,this.imagUnit) | |
| def +(that: Int) = ComplexNumber(this.real+that,this.imag,this.imagUnit) | |
| def +(that: Long) = ComplexNumber(this.real+that,this.imag,this.imagUnit) | |
| def +(that: Float) = ComplexNumber(this.real+that,this.imag,this.imagUnit) | |
| def +(that: Double) = ComplexNumber(this.real+that,this.imag,this.imagUnit) | |
| def -(that: ComplexNumber) = ComplexNumber(this.real-that.real,this.imag-that.imag,this.imagUnit) | |
| def -(that: Int) = ComplexNumber(this.real-that,this.imag,this.imagUnit) | |
| def -(that: Long) = ComplexNumber(this.real-that,this.imag,this.imagUnit) | |
| def -(that: Float) = ComplexNumber(this.real-that,this.imag,this.imagUnit) | |
| def -(that: Double) = ComplexNumber(this.real-that,this.imag,this.imagUnit) | |
| def *(that: ComplexNumber) = ComplexNumber(this.real*that.real - this.imag*that.imag, this.real*that.imag+this.imag*that.real,this.imagUnit) | |
| def *(that: Int) = ComplexNumber(this.real*that,this.imag*that,this.imagUnit) | |
| def *(that: Long) = ComplexNumber(this.real*that,this.imag*that,this.imagUnit) | |
| def *(that: Float) = ComplexNumber(this.real*that,this.imag*that,this.imagUnit) | |
| def *(that: Double) = ComplexNumber(this.real*that,this.imag*that,this.imagUnit) | |
| def /(that: ComplexNumber) = { | |
| val xnorm = that.real*that.real+that.imag*that.imag | |
| ComplexNumber((this.real*that.real+this.imag*that.imag)/xnorm,(this.imag*that.real-this.real*that.imag)/xnorm,this.imagUnit) | |
| } | |
| def /(that: Int) = ComplexNumber(this.real/that,this.imag/that,this.imagUnit) | |
| def /(that: Long) = ComplexNumber(this.real/that,this.imag/that,this.imagUnit) | |
| def /(that: Float) = ComplexNumber(this.real/that,this.imag/that,this.imagUnit) | |
| def /(that: Double) = ComplexNumber(this.real/that,this.imag/that,this.imagUnit) | |
| // 複素数の剰余計算というものが定義されているのかどうかわかりませんが、書いてみました。 | |
| // この部分はBreezeの実装とは異なります。 | |
| def %(that: ComplexNumber) = { | |
| val div = this./(that) | |
| this - ComplexNumber(Math.round(div.re()),Math.round(div.im()),this.imagUnit)*that | |
| } | |
| def %(that: Int): ComplexNumber = this.%(ComplexNumber(that, 0, this.imagUnit)) | |
| def %(that: Long): ComplexNumber = %(ComplexNumber(that, 0, this.imagUnit)) | |
| def %(that: Float): ComplexNumber = %(ComplexNumber(that, 0, this.imagUnit)) | |
| def %(that: Double): ComplexNumber = %(ComplexNumber(that, 0, this.imagUnit)) | |
| def unary_- = ComplexNumber(-real,-imag,this.imagUnit) | |
| def abs = math.sqrt(real*real+imag*imag) | |
| def conjugate = ComplexNumber(real,-imag,this.imagUnit) | |
| def log = ComplexNumber(math.log(abs),math.atan2(imag,real),this.imagUnit) | |
| def exp = { | |
| val expreal = math.exp(real) | |
| ComplexNumber(expreal*math.cos(imag),expreal*math.sin(imag),this.imagUnit) | |
| } | |
| def pow(that: Int): ComplexNumber = pow(ComplexNumber(that,0,this.imagUnit)) | |
| def pow(that: Double): ComplexNumber = pow(ComplexNumber(that,0,this.imagUnit)) | |
| def pow(that: ComplexNumber): ComplexNumber = { | |
| if (that == ComplexNumber.zero) ComplexNumber.one | |
| else if (this == ComplexNumber.zero) { | |
| if (that.imag != 0.0 || that.real < 0.0) ComplexNumber.nan | |
| else ComplexNumber.zero | |
| } else { | |
| val c = log * that | |
| val expReal = math.exp(c.real) | |
| ComplexNumber(expReal*math.cos(c.imag),expReal*math.sin(c.imag),this.imagUnit) | |
| } | |
| } | |
| // こんなのも定義してみます。 | |
| def **(that: ComplexNumber): ComplexNumber = pow(that) | |
| def **(that: Double): ComplexNumber = pow(that) | |
| def **(that: Int): ComplexNumber = pow(that) | |
| override def equals(that: Any) = that match { | |
| case that: ComplexNumber => this.real == that.real && this.imag == that.imag | |
| case real: Double => this.real == real && this.imag == 0 | |
| case real: Int => this.real == real && this.imag == 0 | |
| case real: Short => this.real == real && this.imag == 0 | |
| case real: Long => this.real == real && this.imag == 0 | |
| case real: Float => this.real == real && this.imag == 0 | |
| case _ => false | |
| } | |
| def >(that: ComplexNumber) = | |
| (this.real > that.real || (this.real == that.real && this.imag > that.imag)) | |
| def >=(that: ComplexNumber) = | |
| (this.real >= that.real || (this.real == that.real && this.imag >= that.imag)) | |
| def <(that: ComplexNumber) = | |
| (this.real < that.real || (this.real == that.real && this.imag < that.imag)) | |
| def <=(that: ComplexNumber) = | |
| (this.real <= that.real || (this.real == that.real && this.imag <= that.imag)) | |
| // 試しにこんな演算子を定義してみます。 | |
| def <>(that: ComplexNumber) = | |
| (this.real != that.real || this.imag != that.imag) | |
| override def hashCode() = real.## ^ imag.## | |
| } | |
| object ComplexNumber { | |
| outer => | |
| val one = new ComplexNumber(1,0) | |
| val zero = new ComplexNumber(0,0) | |
| val imaginaryUnit = new ComplexNumber(0,1) | |
| val nan = new ComplexNumber(Double.NaN,Double.NaN) | |
| // Javaでいうところのstaticなメソッドみたいなものです。 | |
| def exp(that: ComplexNumber): ComplexNumber = that.exp | |
| def log(that: ComplexNumber): ComplexNumber = that.log | |
| // 実数に複素数を作用させる演算が定義されていなかったので、追加しました。 | |
| // 試行錯誤の末、以下の一行になりました… | |
| implicit def fromDouble(d: Double) = new ComplexNumber(d) | |
| } | |
| } | |
| object ComplexNumber { | |
| outer => | |
| val one = new ComplexNumber(1,0) | |
| val zero = new ComplexNumber(0,0) | |
| val imaginaryUnit = new ComplexNumber(0,1) | |
| val nan = new ComplexNumber(Double.NaN,Double.NaN) | |
| // Javaでいうところのstaticなメソッドみたいな使い方ができそうです。 | |
| def exp(that: ComplexNumber): ComplexNumber = that.exp | |
| def log(that: ComplexNumber): ComplexNumber = that.log | |
| } |
by 主な変更点
Breezeの実装から変更した点のうち、主なものは以下の通りです。
- 複素数を扱うためのオブジェクト及びクラスの名前自体をComplexからComplexNumberに変更しています。
- toStringメソッドで虚数成分が負の複素数を表示する際に”3+-2i”のような形ではなく、”3-2i”のように符号を考慮した文字列を返すように変更しています。また、虚数成分が0の場合には実数成分のみをString型に変換するように変更しています。
- 虚数単位として通常使われる
- 複素数の剰余計算を行う際に除算を行うが、その結果得られた複素数の実数成分及び虚数成分の整数への丸め方を四捨五入で行うように変更しました。
- べき乗の演算子として”**”を、等しくないことを示す演算子として”<>”を定義しました。
- オブジェクトの定義の方にexp及びlogをJavaでいうところのstaticメソッド的な使い方ができるメソッドを定義してみました。
最初の実装にはなかったものの、後から追加した点
- ComplexNumberのコンストラクタの引数のうち、imagのデフォルト値を設定しました。
- 実数に複素数を作用させる演算に対応できていなかったので、対応するためのコードを追加しました。
できていない点
できていない点は以下の通りです。
- Double型等のequalsメソッドがComplexNumber型を扱えるようにするための機能追加。ScalaのDoubleクラスがfinalであることに気がつかず、equalsメソッドがoverrideできないことと、equalsメソッドの引数がAny型であるために、implicitな型変換の際に
override def equals(that: Any) …
的なコードを書いてもこのコードを見に来てはくれないことに気づくまでに2日ほど、未練を断ち切るまでにさらに1日ほどかかってしまいました。(´・ω・｀)
まとめ
ここまで、Eclipse上でScalaで複素数を扱うクラス及びその動作確認を行うためのコードを習作的に書いてみました。これをEclipseなしで有用なアプリケーションとして動かすためには、アプリケーションをビルドするためのソフトウェアや、コードをテストするためのプログラム及びソフトウェアが必要になります。それらの使い方については次の記事で書きます。
複素数の計算結果を確認するための検算が大変そうです。ちょっとサボっちゃおうかな…
この記事は以上です。
Eclipse+SBTでScalaのテストコードを書いて動かそうとしたところ、かなりハマったのでメモ。 
Eclipse+SBTで実行用JARファイルをビルドして、スタンドアロンで動かしてみた。 
JavaのリストをScalaのリストに変換しようとしたところ、割と盛大にハマったのでメモ。 
Play framework (2.7.3)を使って構築したWebアプリケーションのカスタムエラーページにmessagesファイルで設定した文字列を表示する。 