はじめに
ここのところScalaの記事が続いていますが、この記事もScala関連になります。
前の記事で、Scalaで複素数を扱うためのオブジェクト及びクラス(以下、単に「クラス等」と書きます。)を書きましたが、これだけだとせっかく書いたクラスを動かすことはできません。
ソフトウェア開発とかソフトウェア工学的には、次のステップとしてナウなヤングにバカうけな一般的なのは「テストコードを書く」ということになるんですけど、本サイトの管理人はどちらかというと早く計算結果だけが知りたい派なので、テストコードの件はいったん脇に置いておくことにします。
そこで、この記事ではEclipseのScalaプロジェクトでmainメソッドを持ったクラスを定義して計算結果を確認する方法について書いていきます。
スポンサーリンク
EclipseのScalaプロジェクトへのオブジェクトの追加
前の記事の「コードを書くための準備」の手順4あたり以降の手順を用いると、main関数を追加するためのオブジェクトを作成できます。
この記事では、下図のように”ComplexNumberMain”オブジェクトを作成したものと仮定します。
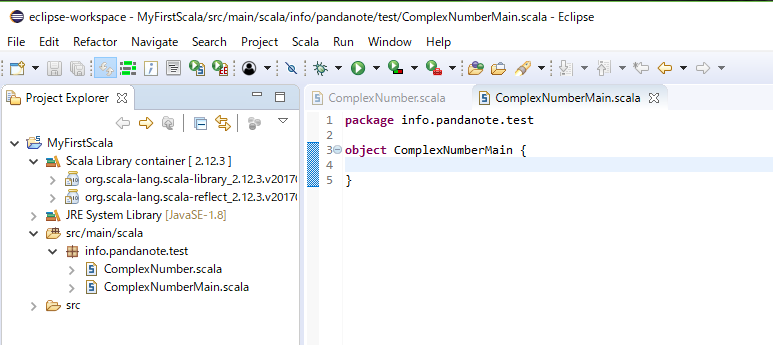
main関数をサクサクと(?)書きます。
前項で作ったオブジェクトにmain関数を書いていきます。以下のようなmain関数を書いてみました。かなり長いです。
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| package info.pandanote.test | |
| // Scalaで複素数を扱うためのテスト用のコード例です。 | |
| // このコードは無保証であり、使用したことよって得られる結果については一切保証いたしません。 | |
| // 詳細は以下のURLを参照いただけると幸いです。 | |
| // https://pandanote.info/?p=1849 | |
| object ComplexNumberTest { | |
| def main(args: Array[String]): Unit = { | |
| val a = ComplexNumber(-2,4) | |
| val b = ComplexNumber(-3,3) | |
| val c = ComplexNumber(5,0) | |
| val d = ComplexNumber(9,-4) | |
| val e = ComplexNumber(4,-1) | |
| val f = -3.000428692900978 | |
| val g = 10 | |
| val aa = ComplexNumber(2,1) | |
| val ab = ComplexNumber(3,-3) | |
| val ac = ComplexNumber(4,5) | |
| val ad = ComplexNumber.one | |
| // toString() | |
| println("--- toString() ---") | |
| println("a="+a.toString) | |
| println("b="+b.toString) | |
| println("c="+c.toString) | |
| println("d="+d.toString) | |
| println("e="+e.toString) | |
| println("aa="+aa.toString) | |
| println("ab="+ab.toString) | |
| println("ac="+ac.toString) | |
| println("ad="+ad.toString) | |
| println(ComplexNumber.one) | |
| println(ComplexNumber.zero) | |
| // re() | |
| println("--- re() ---") | |
| println("Re(a) = "+a.re.toString) | |
| println("Re(b) = "+b.re.toString) | |
| println("Re(c) = "+c.re.toString) | |
| println("Re(d) = "+d.re.toString) | |
| println("Re(e) = "+e.re.toString) | |
| println("Re(aa) = "+aa.re.toString) | |
| println("Re(ab) = "+ab.re.toString) | |
| println("Re(ac) = "+ac.re.toString) | |
| println("Re(ad) = "+ad.re.toString) | |
| println("Re(ComplexNumber.one) = "+ComplexNumber.one.re.toString) | |
| // im() | |
| println("--- im() ---") | |
| println("Im(a) = "+a.im.toString) | |
| println("Im(b) = "+b.im.toString) | |
| println("Im(c) = "+c.im.toString) | |
| println("Im(d) = "+d.im.toString) | |
| println("Im(e) = "+e.im.toString) | |
| println("Im(aa) = "+aa.im.toString) | |
| println("Im(ab) = "+ab.im.toString) | |
| println("Im(ac) = "+ac.im.toString) | |
| println("Im(ad) = "+ad.im.toString) | |
| println("Im(ComplexNumber.imaginaryUnit) = "+ComplexNumber.imaginaryUnit.im.toString) | |
| // +(that: ComplexNumber) | |
| println("--- +(that: ComplexNumber) ---") | |
| println("a + b = "+(a + b).toString) | |
| println("b + c = "+(b + c).toString) | |
| println("c + d = "+(c + d).toString) | |
| println("d + e = "+(d + e).toString) | |
| println("aa + 1 = "+(aa+ComplexNumber.one).toString) | |
| // +(that: Int) | |
| println("--- +(that: Int) ---") | |
| println("a + 2 = "+(a + 2).toString) | |
| println("b + 3 = "+(b + 3).toString) | |
| println("c + 4 = "+(c + 4).toString) | |
| println("d + 5 = "+(d + 5).toString) | |
| println("e + 6 = "+(d + 6).toString) | |
| // +(that: Long) | |
| println("--- +(that: Long) ---") | |
| println("a + 2L = "+(a + 2L).toString) | |
| println("b + 4L = "+(b + 4L).toString) | |
| println("c + 8L = "+(c + 8L).toString) | |
| println("d + 16L = "+(d + 16L).toString) | |
| println("e + 32L = "+(e + 32L).toString) | |
| // +(that: Float) | |
| println("--- +(that: Float) ---") | |
| println("a + 0.1f = "+(a + 0.1f).toString) | |
| println("b + 0.2f = "+(b + 0.2f).toString) | |
| println("c + 0.3f = "+(c + 0.3f).toString) | |
| println("d + 0.4f = "+(d + 0.4f).toString) | |
| println("e + 0.5f = "+(e + 0.5f).toString) | |
| // +(that: Double) | |
| println("--- +(that: Double) ---") | |
| println("a + 0.3 = "+(a + 0.3).toString) | |
| println("b + 0.6 = "+(b + 0.6).toString) | |
| println("c + 0.9 = "+(c + 0.9).toString) | |
| println("d + 1.2 = "+(d + 1.2).toString) | |
| println("e + 1.5 = "+(e + 1.5).toString) | |
| // -(that: ComplexNumber) | |
| println("--- -(that: ComplexNumber) ---") | |
| println("a - b = "+(a - b).toString) | |
| println("b - c = "+(b - c).toString) | |
| println("c - d = "+(c - d).toString) | |
| println("d - e = "+(d - e).toString) | |
| println("aa - ab = "+(aa - ab).toString) | |
| // -(that: Int) | |
| println("--- -(that: Int) ---") | |
| println("a - 2 = "+(a - 2).toString) | |
| println("b - 3 = "+(b - 3).toString) | |
| println("c - 4 = "+(c - 4).toString) | |
| println("d - 5 = "+(d - 5).toString) | |
| println("e - 6 = "+(e - 6).toString) | |
| // -(that: Long) | |
| println("--- -(that: Long) ---") | |
| println("a - 1L = "+(a - 1L).toString) | |
| println("b - 2L = "+(b - 2L).toString) | |
| println("c - 4L = "+(c - 4L).toString) | |
| println("d - 8L = "+(d - 8L).toString) | |
| println("e - 16L = "+(e - 16L).toString) | |
| // -(that: Float) | |
| println("--- -(that: Float) ---") | |
| println("a - 0.1f = "+(a - 0.1f).toString) | |
| println("b - 0.2f = "+(b - 0.2f).toString) | |
| println("c - 0.3f = "+(c - 0.3f).toString) | |
| println("d - 0.4f = "+(d - 0.4f).toString) | |
| println("e - 0.5f = "+(e - 0.5f).toString) | |
| // -(that: Double) | |
| println("--- -(that: Double) ---") | |
| println("a - 0.3 = "+(a - 0.3).toString) | |
| println("b - 0.6 = "+(b - 0.6).toString) | |
| println("c - 0.9 = "+(c - 0.9).toString) | |
| println("d - 1.2 = "+(d - 1.2).toString) | |
| println("e - 1.5 = "+(e - 1.5).toString) | |
| // *(that: ComplexNumber) | |
| println("--- *(that: ComplexNumber) ---") | |
| println("a * b = "+(a * b).toString) | |
| println("b * c = "+(b * c).toString) | |
| println("c * d = "+(c * d).toString) | |
| println("d * e = "+(d * e).toString) | |
| println("aa * ac = "+(aa*ac).toString) | |
| // *(that: Int) | |
| println("--- *(that: Int) ---") | |
| println("a * 2 = "+(a * 2).toString) | |
| println("b * 3 = "+(b * 3).toString) | |
| println("c * 4 = "+(c * 4).toString) | |
| println("d * 5 = "+(d * 5).toString) | |
| println("e * 6 = "+(e * 6).toString) | |
| // *(that: Long) | |
| println("--- *(that: Long) ---") | |
| println("a * 7L = "+(a * 7L).toString) | |
| println("b * 8L = "+(b * 8L).toString) | |
| println("c * 9L = "+(c * 9L).toString) | |
| println("d * 10L = "+(d * 10L).toString) | |
| println("e * 11L = "+(e * 11L).toString) | |
| // *(that: Float) | |
| println("--- *(that: Float) ---") | |
| println("a * 0.2f = "+(a * 0.2f).toString) | |
| println("b * 0.3f = "+(b * 0.3f).toString) | |
| println("c * 0.4f = "+(c * 0.4f).toString) | |
| println("d * 0.5f = "+(d * 0.5f).toString) | |
| println("e * 0.6f = "+(e * 0.6f).toString) | |
| // *(that: Double) | |
| println("--- *(that: Double) ---") | |
| println("a * 0.2 = "+(a * 0.2).toString) | |
| println("b * 0.3 = "+(b * 0.3).toString) | |
| println("c * 0.4 = "+(c * 0.4).toString) | |
| println("d * 0.5 = "+(d * 0.5).toString) | |
| println("e * 0.6 = "+(e * 0.6).toString) | |
| // /(that: ComplexNumber) | |
| println("--- /(that: ComplexNumber) ---") | |
| println("a / b = "+(a / b).toString) | |
| println("b / c = "+(b / c).toString) | |
| println("c / d = "+(c / d).toString) | |
| println("d / e = "+(d / e).toString) | |
| println("aa / ab = "+(aa/ab).toString) | |
| // /(that: Int) | |
| println("--- /(that: Int) ---") | |
| println("a / 2 = "+(a / 2).toString) | |
| println("b / 3 = "+(b / 3).toString) | |
| println("c / 4 = "+(c / 4).toString) | |
| println("d / 5 = "+(d / 5).toString) | |
| println("e / 6 = "+(e / 6).toString) | |
| println("ab / 4 = "+(ab / 4).toString) | |
| // /(that: Long) | |
| println("--- /(that: Long) ---") | |
| println("a / 6L = "+(a / 6L).toString) | |
| println("b / 5L = "+(b / 5L).toString) | |
| println("c / 4L = "+(c / 4L).toString) | |
| println("d / 3L = "+(d / 3L).toString) | |
| println("e / 2L = "+(e / 2L).toString) | |
| // /(that: Float) | |
| println("--- /(that: Float) ---") | |
| println("a / 0.5f = "+(a / 0.5f).toString) | |
| println("b / 0.6f = "+(b / 0.6f).toString) | |
| println("c / 0.7f = "+(c / 0.7f).toString) | |
| println("d / 0.8f = "+(d / 0.8f).toString) | |
| println("e / 0.9f = "+(e / 0.9f).toString) | |
| // /(that: Double) | |
| println("--- /(that: Double) ---") | |
| println("a / 1.1 = "+(a / 1.1).toString) | |
| println("b / 1.2 = "+(b / 1.2).toString) | |
| println("c / 1.3 = "+(c / 1.3).toString) | |
| println("d / 1.4 = "+(d / 1.4).toString) | |
| println("e / 1.5 = "+(e / 1.5).toString) | |
| // %(that: ComplexNumber) | |
| println("--- %(that: ComplexNumber) ---") | |
| println("a % b = "+(a % b).toString) | |
| println("b % c = "+(b % c).toString) | |
| println("c % d = "+(c % d).toString) | |
| println("d % e = "+(d % e).toString) | |
| // %(that: Int) | |
| println("--- %(that: Int) ---") | |
| println("a % 5 = "+(a % 5).toString) | |
| println("b % 6 = "+(b % 6).toString) | |
| println("c % 7 = "+(c % 7).toString) | |
| println("d % 8 = "+(d % 8).toString) | |
| println("ab % 4 = "+(ab % 4).toString) | |
| // %(that: Long) | |
| println("--- %(that: Long) ---") | |
| println("a % 5L = "+(a % 5L).toString) | |
| println("b % 6L = "+(b % 6L).toString) | |
| println("c % 7L = "+(c % 7L).toString) | |
| println("d % 8L = "+(d % 8L).toString) | |
| println("e % 4L = "+(e % 9L).toString) | |
| // %(that: Float) | |
| println("--- %(that: Float) ---") | |
| println("a % 1.5f = "+(a % 1.5f).toString) | |
| println("b % 2.0f = "+(b % 2.0f).toString) | |
| println("c % 2.5f = "+(c % 2.5f).toString) | |
| println("d % 3.0f = "+(d % 3.0f).toString) | |
| println("e % 4.0f = "+(e % 4.0f).toString) | |
| // %(that: Double) | |
| println("--- %(that: Double) ---") | |
| println("a % 1.5 = "+(a % 1.5).toString) | |
| println("b % 2.0 = "+(b % 2.0).toString) | |
| println("c % 2.5 = "+(c % 2.5).toString) | |
| println("d % 3.0 = "+(d % 3.0).toString) | |
| println("e % 4.0 = "+(d % 4.0).toString) | |
| // unary_- = ComplexNumber(-real,-imag,this.imagUnit) | |
| println("--- unary_- ---") | |
| println("-a = "+(-a).toString) | |
| println("-b = "+(-b).toString) | |
| println("-c = "+(-c).toString) | |
| println("-d = "+(-d).toString) | |
| println("-e = "+(-e).toString) | |
| // abs = math.sqrt(real*real+imag*imag) | |
| println("--- abs ---") | |
| println("a.abs = "+a.abs.toString) | |
| println("b.abs = "+b.abs.toString) | |
| println("c.abs = "+c.abs.toString) | |
| println("d.abs = "+d.abs.toString) | |
| println("e.abs = "+e.abs.toString) | |
| // conjugate = ComplexNumber(real,-imag,this.imagUnit) | |
| println("--- conjugate ---") | |
| println("a.conjugate = "+a.conjugate.toString) | |
| println("b.conjugate = "+b.conjugate.toString) | |
| println("c.conjugate = "+c.conjugate.toString) | |
| println("d.conjugate = "+d.conjugate.toString) | |
| println("e.conjugate = "+e.conjugate.toString) | |
| println("aa.conjugate*(ac-ComplexNumber.one*7) = "+(aa.conjugate*(ac-ComplexNumber.one*7)).toString) | |
| // log = ComplexNumber(math.log(abs)) | |
| println("--- log ---") | |
| println("a.log = "+a.log.toString) | |
| println("b.log = "+b.log.toString) | |
| println("c.log = "+c.log.toString) | |
| println("d.log = "+d.log.toString) | |
| println("e.log = "+e.log.toString) | |
| // exp = { | |
| println("--- exp ---") | |
| println("a.exp = "+a.exp.toString) | |
| println("b.exp = "+b.exp.toString) | |
| println("c.exp = "+c.exp.toString) | |
| println("d.exp = "+d.exp.toString) | |
| println("e.exp = "+e.exp.toString) | |
| println("aa.exp = "+aa.exp.toString) | |
| println("aa.exp.log = "+aa.exp.log.toString) | |
| println("aa.exp.log != aa: "+(aa.exp.log == aa)) | |
| // pow(that: Double) | |
| println("--- pow(that: Double) ---") | |
| println("a pow 0.2 = "+(a pow 0.2).toString) | |
| println("b pow 0.4 = "+(b pow 0.4).toString) | |
| println("c pow 0.6 = "+(c pow 0.6).toString) | |
| println("d pow 0.8 = "+(d pow 0.8).toString) | |
| println("e pow 1.1 = "+(e pow 1.1).toString) | |
| println("a.pow(0.2) = "+a.pow(0.2).toString) | |
| println("b.pow(0.4) = "+b.pow(0.4).toString) | |
| println("c.pow(0.6) = "+c.pow(0.6).toString) | |
| println("d.pow(0.8) = "+d.pow(0.8).toString) | |
| println("e.pow(1.1) = "+e.pow(1.1).toString) | |
| // pow(that: Int) | |
| println("--- pow(that: Int) ---") | |
| println("aa.pow(3) = "+aa.pow(3).toString) | |
| // pow(that: ComplexNumber) | |
| println("--- pow(that: ComplexNumber) ---") | |
| println("a pow b = "+(a pow b).toString) | |
| println("b pow c = "+(b pow c).toString) | |
| println("c pow d = "+(c pow d).toString) | |
| println("d pow e = "+(d pow e).toString) | |
| println("e pow a = "+(e pow a).toString) | |
| println("a.pow(b) = "+a.pow(b).toString) | |
| println("b.pow(c) = "+b.pow(c).toString) | |
| println("c.pow(d) = "+c.pow(d).toString) | |
| println("d.pow(e) = "+d.pow(e).toString) | |
| println("e.pow(a) = "+e.pow(a).toString) | |
| println("aa.pow(aa) = "+aa.pow(aa).toString) | |
| // **(that: ComplexNumber) | |
| println("--- **(that: ComplexNumber) ---") | |
| println("a ** b = "+(a ** b).toString) | |
| println("b ** c = "+(b ** c).toString) | |
| println("c ** d = "+(c ** d).toString) | |
| println("d ** e = "+(d ** e).toString) | |
| println("e ** a = "+(d ** e).toString) | |
| println("aa ** ab = "+(aa**ab).toString) | |
| // **(that: Double) | |
| println("--- **(that: Double) ---") | |
| println("a ** 0.2 = "+(a ** 0.2).toString) | |
| println("b ** 0.4 = "+(b ** 0.4).toString) | |
| println("c ** 0.6 = "+(c ** 0.6).toString) | |
| println("d ** 0.8 = "+(d ** 0.8).toString) | |
| println("e ** 1.1 = "+(e ** 1.1).toString) | |
| // **(that: Int) | |
| println("--- **(that: Int) ---") | |
| println("aa ** 2 = "+(aa ** 2).toString) | |
| // equals(that: Any) | |
| println("--- equals(that: Any) ---") | |
| println("a equals b: "+(a equals b).toString) | |
| println("b equals c: "+(b equals c).toString) | |
| println("c equals d: "+(c equals d).toString) | |
| println("d equals e: "+(d equals e).toString) | |
| println("e equals a: "+(e equals a).toString) | |
| println("a equals a: "+(a equals a).toString) | |
| println("b equals b: "+(b equals b).toString) | |
| println("c equals c: "+(c equals c).toString) | |
| println("d equals d: "+(d equals d).toString) | |
| println("e equals e: "+(e equals e).toString) | |
| println("ad == 1: "+(ad == 1).toString) | |
| println("ad.equals(1): "+ad.equals(1)) | |
| println("aa != aa: "+(aa!=aa)) | |
| // >(that: ComplexNumber) | |
| println("--- >(that: ComplexNumber) ---") | |
| println("a > b: "+(a > b).toString) | |
| println("b > c: "+(b > c).toString) | |
| println("c > d: "+(c > d).toString) | |
| println("d > e: "+(d > e).toString) | |
| println("aa > ab: "+(aa > ab).toString) | |
| // >=(that: ComplexNumber) | |
| println("--- >=(that: ComplexNumber) ---") | |
| println("a >= b: "+(a >= b).toString) | |
| println("b >= c: "+(b >= c).toString) | |
| println("c >= d: "+(c >= d).toString) | |
| println("d >= e: "+(d >= e).toString) | |
| // <(that: ComplexNumber) | |
| println("--- <(that: ComplexNumber) ---") | |
| println("a < b: "+(a < b).toString) | |
| println("b < c: "+(b < c).toString) | |
| println("c < d: "+(c < d).toString) | |
| println("d < e: "+(d < e).toString) | |
| println("aa < ab: "+(aa < ab).toString) | |
| // <=(that: ComplexNumber) | |
| println("--- <=(that: ComplexNumber) ---") | |
| println("a <= b: "+(a <= b).toString) | |
| println("b <= c: "+(b <= c).toString) | |
| println("c <= d: "+(c <= d).toString) | |
| println("d <= e: "+(d <= e).toString) | |
| // <>(that: ComplexNumber) | |
| println("--- <>(that: ComplexNumber) ---") | |
| println("a <> b: "+(a <> b).toString) | |
| println("b <> c: "+(b <> c).toString) | |
| println("c <> d: "+(c <> d).toString) | |
| println("d <> e: "+(d <> e).toString) | |
| println("aa <> aa: "+(aa<>aa).toString) | |
| // exp(that: ComplexNumber) | |
| println("--- ComplexNumber.exp(that: ComplexNumber)---") | |
| println("ComplexNumber.exp(a) = "+ComplexNumber.exp(a).toString) | |
| println("ComplexNumber.exp(b) = "+ComplexNumber.exp(b).toString) | |
| println("ComplexNumber.exp(c) = "+ComplexNumber.exp(c).toString) | |
| println("ComplexNumber.exp(d) = "+ComplexNumber.exp(d).toString) | |
| println("ComplexNumber.exp(e) = "+ComplexNumber.exp(e).toString) | |
| println("ComplexNumber.exp(aa) = "+ComplexNumber.exp(aa).toString) | |
| // log(that: ComplexNumber) | |
| println("--- ComplexNumber.log(that: ComplexNumber)---") | |
| println("ComplexNumber.log(a) = "+ComplexNumber.log(a).toString) | |
| println("ComplexNumber.log(b) = "+ComplexNumber.log(b).toString) | |
| println("ComplexNumber.log(c) = "+ComplexNumber.log(c).toString) | |
| println("ComplexNumber.log(d) = "+ComplexNumber.log(d).toString) | |
| println("ComplexNumber.log(e) = "+ComplexNumber.log(e).toString) | |
| // Imaginary Unit and others. | |
| println("--- Imaginary Unit and others. ---") | |
| val aj = new ComplexNumber(2,-5,"j") | |
| println("aj = "+aj) | |
| println("aj * aa = "+(aj*aa).toString) | |
| println("aa * aj = "+(aa*aj).toString) | |
| println("aj.pow(0) = "+aj.pow(0)) | |
| println("aj.pow(2) = "+aj.pow(2)) | |
| println("aj * aj = "+(aj*aj)) | |
| println("aj.pow(2).log = "+aj.pow(2).log) | |
| println("aj.pow(2).pow(0.5) = "+aj.pow(2).pow(0.5)) | |
| } | |
| } |
by 演算子関連の動作を確認するためのテストコードの量が多すぎて最初から手で書くレベルではなさそうだったので、以下の手順で作りました。
- Python3で元のコード(ComplexNumberクラス等)の”def”の行を取り出して、それを元にテンプレート的なコードを書き出すためのスクリプトを作成します。
- 手順1で作成したプログラムを実行し、Scalaのプログラムのテンプレート的なものを作ります。
- 手順2で作成したプログラムを修正します。すると上記のプログラムが出来上がります。
プログラムを実行する。
前節のプログラムをEclipse上で実行してみます。Eclipseを起動して、前節のプログラムをProject Explorer上で右クリックすると、ポップアップメニューが表示されますので、「Run As」→「Scala Application」と選択していきます(下図)。
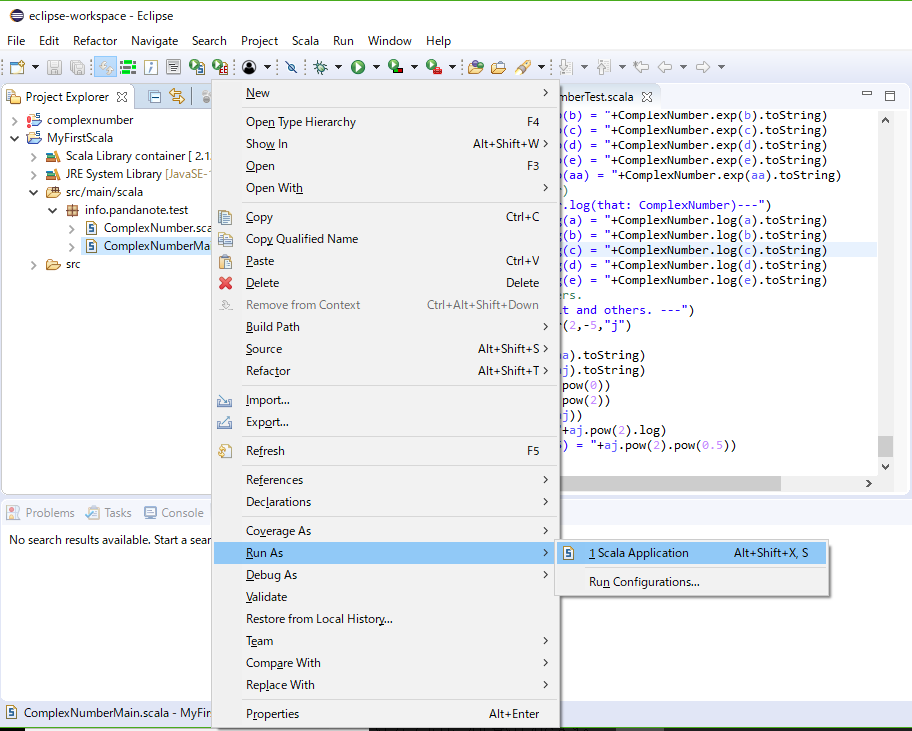
すると、プログラムが実行されてEclipseのConsoleビューに実行結果が以下のように表示されます。
— toString() —
a=-2.0+4.0i
b=-3.0+3.0i
c=5.0
d=9.0-4.0i
e=4.0-1.0i
aa=2.0+1.0i
ab=3.0-3.0i
ac=4.0+5.0i
ad=1.0
1.0
0.0
— re() —
Re(a) = -2.0
Re(b) = -3.0
Re(c) = 5.0
Re(d) = 9.0
Re(e) = 4.0
Re(aa) = 2.0
Re(ab) = 3.0
Re(ac) = 4.0
Re(ad) = 1.0
Re(ComplexNumber.one) = 1.0
— im() —
Im(a) = 4.0
Im(b) = 3.0
Im(c) = 0.0
Im(d) = -4.0
Im(e) = -1.0
Im(aa) = 1.0
Im(ab) = -3.0
Im(ac) = 5.0
Im(ad) = 0.0
Im(ComplexNumber.imaginaryUnit) = 1.0
— +(that: ComplexNumber) —
a + b = -5.0+7.0i
b + c = 2.0+3.0i
c + d = 14.0-4.0i
d + e = 13.0-5.0i
aa + 1 = 3.0+1.0i
— +(that: Int) —
a + 2 = 0.0+4.0i
b + 3 = 0.0+3.0i
c + 4 = 9.0
d + 5 = 14.0-4.0i
e + 6 = 15.0-4.0i
— +(that: Long) —
a + 2L = 0.0+4.0i
b + 4L = 1.0+3.0i
c + 8L = 13.0
d + 16L = 25.0-4.0i
e + 32L = 36.0-1.0i
— +(that: Float) —
a + 0.1f = -1.8999999985098839+4.0i
b + 0.2f = -2.7999999970197678+3.0i
c + 0.3f = 5.300000011920929
d + 0.4f = 9.400000005960464-4.0i
e + 0.5f = 4.5-1.0i
— +(that: Double) —
a + 0.3 = -1.7+4.0i
b + 0.6 = -2.4+3.0i
c + 0.9 = 5.9
d + 1.2 = 10.2-4.0i
e + 1.5 = 5.5-1.0i
— -(that: ComplexNumber) —
a – b = 1.0+1.0i
b – c = -8.0+3.0i
c – d = -4.0+4.0i
d – e = 5.0-3.0i
aa – ab = -1.0+4.0i
— -(that: Int) —
a – 2 = -4.0+4.0i
b – 3 = -6.0+3.0i
c – 4 = 1.0
d – 5 = 4.0-4.0i
e – 6 = -2.0-1.0i
— -(that: Long) —
a – 1L = -3.0+4.0i
b – 2L = -5.0+3.0i
c – 4L = 1.0
d – 8L = 1.0-4.0i
e – 16L = -12.0-1.0i
— -(that: Float) —
a – 0.1f = -2.100000001490116+4.0i
b – 0.2f = -3.2000000029802322+3.0i
c – 0.3f = 4.699999988079071
d – 0.4f = 8.599999994039536-4.0i
e – 0.5f = 3.5-1.0i
— -(that: Double) —
a – 0.3 = -2.3+4.0i
b – 0.6 = -3.6+3.0i
c – 0.9 = 4.1
d – 1.2 = 7.8-4.0i
e – 1.5 = 2.5-1.0i
— *(that: ComplexNumber) —
a * b = -6.0-18.0i
b * c = -15.0+15.0i
c * d = 45.0-20.0i
d * e = 32.0-25.0i
aa * ac = 3.0+14.0i
— *(that: Int) —
a * 2 = -4.0+8.0i
b * 3 = -9.0+9.0i
c * 4 = 20.0
d * 5 = 45.0-20.0i
e * 6 = 24.0-6.0i
— *(that: Long) —
a * 7L = -14.0+28.0i
b * 8L = -24.0+24.0i
c * 9L = 45.0
d * 10L = 90.0-40.0i
e * 11L = 44.0-11.0i
— *(that: Float) —
a * 0.2f = -0.4000000059604645+0.800000011920929i
b * 0.3f = -0.9000000357627869+0.9000000357627869i
c * 0.4f = 2.0000000298023224
d * 0.5f = 4.5-2.0i
e * 0.6f = 2.4000000953674316-0.6000000238418579i
— *(that: Double) —
a * 0.2 = -0.4+0.8i
b * 0.3 = -0.8999999999999999+0.8999999999999999i
c * 0.4 = 2.0
d * 0.5 = 4.5-2.0i
e * 0.6 = 2.4-0.6i
— /(that: ComplexNumber) —
a / b = 1.0-0.3333333333333333i
b / c = -0.6+0.6i
c / d = 0.4639175257731959+0.20618556701030927i
d / e = 2.3529411764705883-0.4117647058823529i
aa / ab = 0.16666666666666666+0.5i
— /(that: Int) —
a / 2 = -1.0+2.0i
b / 3 = -1.0+1.0i
c / 4 = 1.25
d / 5 = 1.8-0.8i
e / 6 = 0.6666666666666666-0.16666666666666666i
ab / 4 = 0.75-0.75i
— /(that: Long) —
a / 6L = -0.3333333333333333+0.6666666666666666i
b / 5L = -0.6+0.6i
c / 4L = 1.25
d / 3L = 3.0-1.3333333333333333i
e / 2L = 2.0-0.5i
— /(that: Float) —
a / 0.5f = -4.0+8.0i
b / 0.6f = -4.999999801317859+4.999999801317859i
c / 0.7f = 7.142857264499277
d / 0.8f = 11.249999832361938-4.999999925494195i
e / 0.9f = 4.444444562182017-1.1111111405455043i
— /(that: Double) —
a / 1.1 = -1.8181818181818181+3.6363636363636362i
b / 1.2 = -2.5+2.5i
c / 1.3 = 3.846153846153846
d / 1.4 = 6.428571428571429-2.857142857142857i
e / 1.5 = 2.6666666666666665-0.6666666666666666i
— %(that: ComplexNumber) —
a % b = 1.0+1.0i
b % c = 2.0-2.0i
c % d = 5.0
d % e = 1.0-2.0i
— %(that: Int) —
a % 5 = -2.0-1.0i
b % 6 = -3.0-3.0i
c % 7 = -2.0
d % 8 = 1.0-4.0i
ab % 4 = -1.0+1.0i
— %(that: Long) —
a % 5L = -2.0-1.0i
b % 6L = -3.0-3.0i
c % 7L = -2.0
d % 8L = 1.0-4.0i
e % 4L = 4.0-1.0i
— %(that: Float) —
a % 1.5f = -0.5-0.5i
b % 2.0f = -1.0-1.0i
c % 2.5f = 0.0
d % 3.0f = 0.0-1.0i
e % 4.0f = 0.0-1.0i
— %(that: Double) —
a % 1.5 = -0.5-0.5i
b % 2.0 = -1.0-1.0i
c % 2.5 = 0.0
d % 3.0 = 0.0-1.0i
e % 4.0 = 1.0
— unary_- —
-a = 2.0-4.0i
-b = 3.0-3.0i
-c = -5.0
-d = -9.0+4.0i
-e = -4.0+1.0i
— abs —
a.abs = 4.47213595499958
b.abs = 4.242640687119285
c.abs = 5.0
d.abs = 9.848857801796104
e.abs = 4.123105625617661
— conjugate —
a.conjugate = -2.0-4.0i
b.conjugate = -3.0-3.0i
c.conjugate = 5.0
d.conjugate = 9.0+4.0i
e.conjugate = 4.0+1.0i
aa.conjugate*(ac-ComplexNumber.one*7) = -1.0+13.0i
— log —
a.log = 1.4978661367769956+2.0344439357957027i
b.log = 1.4451858789480823+2.356194490192345i
c.log = 1.6094379124341003
d.log = 2.2873554892516914-0.41822432957922906i
e.log = 1.416606672028108-0.24497866312686414i
— exp —
a.exp = -0.08846104456538201-0.10242208005667372i
b.exp = -0.04928882411191869+0.00702595148935012i
c.exp = 148.4131591025766
d.exp = -5296.529118582112+6132.434136078618i
e.exp = 29.49950635904248-45.94275907707917i
aa.exp = 3.992324048441272+6.217676312367968i
aa.exp.log = 2.0+1.0i
aa.exp.log != aa: true
— pow(that: Double) —
a pow 0.2 = 1.2391227282494208+0.533984145234475i
b pow 0.4 = 1.0477874354927301+1.4421556827090496i
c pow 0.6 = 2.626527804403767
d pow 0.8 = 5.887527513943062-2.0467970763670778i
e pow 1.1 = 4.579136276791019-1.264732948760852i
a.pow(0.2) = 1.2391227282494208+0.533984145234475i
b.pow(0.4) = 1.0477874354927301+1.4421556827090496i
c.pow(0.6) = 2.626527804403767
d.pow(0.8) = 5.887527513943062-2.0467970763670778i
e.pow(1.1) = 4.579136276791019-1.264732948760852i
— pow(that: Int) —
aa.pow(3) = 2.0000000000000018+11.000000000000002i
— pow(that: ComplexNumber) —
a pow b = -9.728932897152134E-7-2.4973670775173493E-5i
b pow c = 971.9999999999986-972.0000000000013i
c pow d = 1929840.5975569494-300686.7699883458i
d pow e = -4231.1551049887785+4522.423994559331i
e pow a = 0.15546111986274969-0.019819005421442715i
a.pow(b) = -9.728932897152134E-7-2.4973670775173493E-5i
b.pow(c) = 971.9999999999986-972.0000000000013i
c.pow(d) = 1929840.5975569494-300686.7699883458i
d.pow(e) = -4231.1551049887785+4522.423994559331i
e.pow(a) = 0.15546111986274969-0.019819005421442715i
aa.pow(aa) = -0.5048246889783188+3.104144076995529i
— **(that: ComplexNumber) —
a ** b = -9.728932897152134E-7-2.4973670775173493E-5i
b ** c = 971.9999999999986-972.0000000000013i
c ** d = 1929840.5975569494-300686.7699883458i
d ** e = -4231.1551049887785+4522.423994559331i
e ** a = -4231.1551049887785+4522.423994559331i
aa ** ab = 23.39151968521679-38.36036198687259i
— **(that: Double) —
a ** 0.2 = 1.2391227282494208+0.533984145234475i
b ** 0.4 = 1.0477874354927301+1.4421556827090496i
c ** 0.6 = 2.626527804403767
d ** 0.8 = 5.887527513943062-2.0467970763670778i
e ** 1.1 = 4.579136276791019-1.264732948760852i
— **(that: Int) —
aa ** 2 = 3.000000000000001+4.0i
— equals(that: Any) —
a equals b: false
b equals c: false
c equals d: false
d equals e: false
e equals a: false
a equals a: true
b equals b: true
c equals c: true
d equals d: true
e equals e: true
ad == 1: true
ad.equals(1): true
aa != aa: false
— >(that: ComplexNumber) —
a > b: true
b > c: false
c > d: false
d > e: true
aa > ab: false
— >=(that: ComplexNumber) —
a >= b: true
b >= c: false
c >= d: false
d >= e: true
— <(that: ComplexNumber) ---
a < b: false
b < c: true
c < d: true
d < e: false
aa < ab: true
--- <=(that: ComplexNumber) ---
a <= b: false
b <= c: true
c <= d: true
d <= e: false
--- <>(that: ComplexNumber) —
a <> b: true
b <> c: true
c <> d: true
d <> e: true
aa <> aa: false
— ComplexNumber.exp(that: ComplexNumber)—
ComplexNumber.exp(a) = -0.08846104456538201-0.10242208005667372i
ComplexNumber.exp(b) = -0.04928882411191869+0.00702595148935012i
ComplexNumber.exp(c) = 148.4131591025766
ComplexNumber.exp(d) = -5296.529118582112+6132.434136078618i
ComplexNumber.exp(e) = 29.49950635904248-45.94275907707917i
ComplexNumber.exp(aa) = 3.992324048441272+6.217676312367968i
— ComplexNumber.log(that: ComplexNumber)—
ComplexNumber.log(a) = 1.4978661367769956+2.0344439357957027i
ComplexNumber.log(b) = 1.4451858789480823+2.356194490192345i
ComplexNumber.log(c) = 1.6094379124341003
ComplexNumber.log(d) = 2.2873554892516914-0.41822432957922906i
ComplexNumber.log(e) = 1.416606672028108-0.24497866312686414i
— Imaginary Unit and others. —
aj = 2.0-5.0j
aj * aa = 9.0-8.0j
aa * aj = 9.0-8.0i
aj.pow(0) = 1.0
aj.pow(2) = -20.99999999999999-19.999999999999993j
aj * aj = -21.0-20.0j
aj.pow(2).log = 3.3672958299864737-2.3805798993650633j
aj.pow(2).pow(0.5) = 1.9999999999999998-4.999999999999999j
結果についてはすべて検証したわけではありませんが、おそらく正しいのではないかと思います。
まとめ
C++で演算子をオーバーロードした場合と同様に、Scalaでも演算子をオーバーロードすると、動作確認のパターンがソースコードの見かけに反して(※個人の感想です。)増大していきます。そんなときにいきなりテストコードを書いてしまって、そこで何か問題が発覚すると原因の切り分けが難しくなってしまい、気力を奪われてしまいがちです。
また、初めてScalaでコードを記述したためにmainメソッドを使ったプログラムの実行方法も確認する必要があったので、「いきなりテストーコードを書く」というのは作業の単位として大きすぎるように感じたので、いったんmainメソッドにテスト用にも使えるコードを記述して動作確認を行うことで、アプローチとしてはダサくてもいいから作業単位を分割して小さくしたというのがいったんmainメソッドを書いた理由です。
というわけで、別の記事でEclipseを使ってテストを行う方法については書いていきますが、いろいろとハマりましたということだけ、先に書いておきます。
この記事は以上ですが、次の記事に続いていくと思います。
Windows 10 HomeのEmacs(26.2)からrgrepを実行したときに、ripgrepが起動されるように設定してみた。 
Play framework (2.7.3)を使って構築したWebアプリケーションのカスタムエラーページにmessagesファイルで設定した文字列を表示する。 
matplotlibで描いた3Dグラフを動画を作って遊んでいるうちに、Python3のProcessPoolExecutorを使うと少し捗ることに気がついた話。
Emacs 27.2をWindows 10のPCにインストールし、ついでにScalaの開発環境を再整備したり等してみた。 