matplotlibで描いた3Dグラフを動画を作って遊んでいるうちに、Python3のProcessPoolExecutorを使うと少し捗ることに気がついた話。🎥

By | 2020年11月29日 , Last update: 2022年8月7日
0 Comment

はじめに

前の記事で本Webサイトの記事をBag-of-Wordsモデルを使ってベクトル化した結果の一部を3Dの棒グラフにして表示させるまでの道のりについて書きました。

前の記事に書いた方法で3Dの棒グラフが表示できることが確認できましたので、この記事ではベクトル化したデータを用いて記事間の類似度を求め、それを3Dの棒グラフで表示し、さらにグラフの表示のための画像を使って動画を作成するまでの道のりについて書きます。

スポンサーリンク

記事間の類似度の計算

記事の特徴量がベクトル化されているので、この記事では記事$\boldsymbol{a}_i$及び$\boldsymbol{a}_j (0 \le i \lt j \lt n)$間の類似度$s_{ij}$をコサイン類似度(\ref{eq:cosine_similarity})式を使って計算することにします。

\begin{align}
s_{ij} &= \frac{\boldsymbol{a}_i\cdot\boldsymbol{a}_j}{\lvert\boldsymbol{a}_i\rvert\cdot\lvert\boldsymbol{a}_j\rvert} \label{eq:cosine_similarity}
\end{align}

なお、$\{ \boldsymbol{a}_i \} (0 \le i \lt n)$の要素は負でない値、それも大半の要素が0であるために$n$次元空間を有効に使えてないんじゃね? とか、大半の要素が0ならば$\boldsymbol{a}_i\cdot\boldsymbol{a}_j = 0$になる$i,j$の組み合わせが頻出する(=直交しまくる)んじゃね? といった懸念事項は置いといて、$i,j$の組み合わせを変えてひたすら計算しまくることにします。

また、$i=j$としたときの$s_{ii}$の値も計算は可能です(1になります。)が、計算結果として自明であることと、可視化の結果(特に三次元による可視化時)の見た目がイマイチな感じになる(三次元の可視化時には$y=x$のところに壁ができます。)ので、計算の対象から除外しました。

コサイン類似度の計算結果の可視化

計算結果の概要

$s_{ij}$を行列で表現すると対角成分がすべて0の下三角行列$S$((\ref{eq:sinmatrix})式)として表現できます。

\begin{align}
S &= \begin{pmatrix}
0 & a_{11} & a_{12} & \cdots & a_{1,n-1} \\
\vdots & 0 & a_{22} & \cdots & a_{2,n-1} \\
\vdots & \ & \ddots & \ddots & \vdots \\
\vdots & \ & \ & 0 & a_{n-2,n-1} \\
0 & \cdots & \cdots & \cdots & 0 \\
\end{pmatrix} \label{eq:sinmatrix}
\end{align}

$\LaTeX$の本に組版例としてよく登場する斜め三点リーダ(\ddots)が使ってみたかっただけです。

なお、$s_{ii} = 1$であることを考慮すると、$S$は((\ref{eq:sinmatrixwithdiag})式)の$S_{\rm (Not\ used\ in\ this\ article)}$のように表現できますが、この記事では$S$は(\ref{eq:sinmatrix})式で表されるものとして以下の考察を進めていきます。

\begin{align}
S_{\rm (Not\ used\ in\ this\ article)} &= \begin{pmatrix}
1 & a_{11} & a_{12} & \cdots & a_{1,n-1} \\
0 & 1 & a_{22} & \cdots & a_{2,n-1} \\
\vdots & \ddots & \ddots & \ddots & \vdots \\
\vdots & \cdots & 0 & 1 & a_{n-2,n-1} \\
0 & \cdots & \cdots & 0 & 1 \\
\end{pmatrix} \label{eq:sinmatrixwithdiag}
\end{align}

二次元による表示

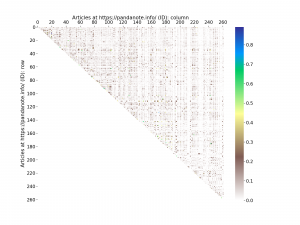
$S$を二次元のヒートマップとして表示すると、下図のような感じになります。

rowとcolumnはよく間違えます。


(クリックすると拡大されて表示されます。)


スポンサーリンク

カラーマップは例によってterrain_rを使用しています(以下同じ)。

上図をよーく見ると、コサイン類似度が大きめの値になっていると思われる緑色や青色の点が(数は少ないですが)存在していることがわかります。

三次元による表示(静止画像)

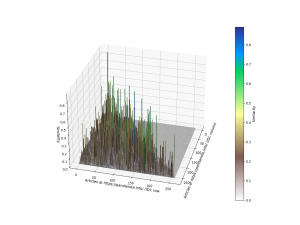
$S$を三次元の棒グラフ(棒ごとの着色は棒が示す値に対応するヒートマップの色で着色しています。)として表示すると、下図のような感じになります。


(クリックすると拡大されて表示されます。)

コサイン類似度が大きめの値になっているところは割とありそうですが、詳細な分析については別途行うことにします。

三次元による表示(動画にしてみた。)

前節の表示では長い棒に隠れてしまっている部分がわかりにくいので、グラフを見る際の視線を少しずつ(1度ずつ)変えた画像を大量に生成し、それらをffmpegで連結した動画(*1)を作成してみます。

作成した動画は棒グラフが1回転するだけの動画ですが、その前に$xy$平面から棒が生えてくる動画を作成し、(*1)の前に連結します。


スポンサーリンク

すると…

以下のような動画ができあがります(BGM入りですので、ご注意願います)。

大事なことなので、2度回転させてます。

見やすくなりましたね(自画自賛)。

動画用の画像生成の効率を上げてみた。

動機

スポンサーリンク

この記事のタイトル的にはここまでは前座で、ここからが本題です。

前節の動画は411枚(50+360+1枚)の画像から構成されています。その内訳は以下の通りです。

  1. $xy$平面から棒が生えてくる部分の動画を構成している画像: 50枚
  2. 棒グラフ全体が1回転(厳密には$359^\circ$)回転する部分の動画を構成している画像: 360枚
  3. 棒グラフ全体を$1^\circ$回転させて回転前の視線に動画を戻すための画像: 1枚

これらの画像を今時のmatplotlibをimportしつつPython3のプログラムで普通に作ろうとすると、1個の論理プロセッサにのみ1個のプロセスが割り当てられるシングルプロセスでの処理になります。


スポンサーリンク

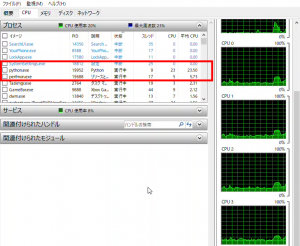
よって、Windows10のリソースモニタで画像生成中のプロセスのCPUの使用率を見ると…

という感じになっていて、画像生成中のプロセスのCPUの使用率は25%になっていることがわかります(上図の赤枠内)。

今時のCPUならノートPC用のものであっても論理プロセッサを複数持つのが当たり前だと思いますので、少なくとも2個、可能ならCPUの持つ全論理プロセッサを画像生成に投入することにより処理の効率を上げて、時短を図りたいところです。

そこで、ProcessPoolExecutorの登場です。

Python3での並列処理のための仕組みはいくつかありますが、子プロセス側から親プロセス側に処理結果を戻す必要がないことと、matplotlibがマルチスレッド対応ではないことから、マルチプロセスでの処理を行うこととしました。

幸いなことにPython3.2から上記の要件を比較的お手軽に実現できるProcessPoolExecutorという仕組みが追加されているので、Python3のプログラム中に以下のように記述してありがたく使わせていただくことにします。🙏

import concurrent.futures as cf

 

コードを書く上での注意事項

ProcessPoolExecutorを使って子プロセスで実行させるコードを記述する場合には、以下の点に注意する必要があります。

親プロセスでのみ実行されるべき処理の記述

子プロセスで実行させる必要のない処理は変数の初期化のための式なども含めて if __name__ = ‘__main__’: の条件式が成立した時にのみ実行されるブロック内に記述します。

ProcessPoolExecutor.map関数への引数の与え方

マルチスレッド処理においては同じ関数を引数(の組)を変えて複数回実行することが一般的ですが、引数(の組)が複数ある場合には、以下の手順でProcessPoolExecutor.map関数の第2引数に与えるべきデータを作成します。

  1. 引数の組の1組分をtupleとしてまとめたものを要素とする配列を作成します。例えば、呼び出し先の関数がfunc(x,y,z)のように3個の引数を持ち、それを3回呼び出す必要があるのであれば、[(x1,y1,z1),(x2,y2,z2),(x3,y3,z3)]のような配列を作成します。
  2. 手順1で作成した配列にアスタリスク(*)を付加してアンパックします。手順1の例ではアンパックをすることによって、配列を1組のtupleを1個の変数とする3個の変数に展開することができます。
  3. 手順2でアンパックした変数をzip関数の入力として与えることで、以下の処理を行います。
    1. tupleの先頭から1個ずつ変数をpopし、それらを取り出し元の変数の順に並べることによって新たなtupleを得る。
    2. 上記の操作を変数として指定されたtupleの要素数と等しい回数だけ繰り返すことによって得られる配列の要素を1個ずつ取り出すことのできるイテレータを作成する。
  4. 手順3で得られたイテレータからは、(x1,x2,x3)、(y1,y2,y3)及び(z1,z2,z3)の3個のtupleをこの順で取り出すことができるので、アスタリスク(*)を使ってアンパックします。

なお、上記の手順の処理は以下のように1行で記述できます。

e.map(func,*zip(*a))

 
上記の記述でeはProcessPoolExecutorを、funcは子スレッドで実行する関数名、aは引数の組の1組分をtupleとしてまとめたものを要素とする配列を表します。

コード例

コード例は以下のような感じになります。

89行目に入力ファイル(転置インデックスをJSON形式で表現したもの。)のデフォルト値が指定されていますが、こちら(@第三倉庫(仮))からダウンロードできます。

所要時間の比較

動画のための画像を生成するためのPython3のプログラムが書けたところで、シングルプロセスとマルチプロセスでそれぞれ411枚の画像の生成処理を実行し、所要時間を比較することにしました。

所要時間は以下の通りです。

  1. シングルプロセスの場合(=ProcessPoolExecutorを使わない場合): 12532.629544秒
  2. マルチプロセスの場合(=ProcessPoolExecutorを使った場合): 6363.661855秒

マルチプロセスで実行すると所要時間がほぼ半分になることがわかりました。

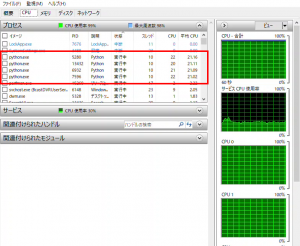
マルチプロセスで実行中のWindows10のリソースモニタで画像生成中のプロセスのCPUの使用率を見ると…

…のような感じ(赤枠)になっていて、プロセスが4個起動しているのですが、所要時間が約1/2にしかなっていません。

CPUのコアのところで何かボトルネックになっているところがありそうですが、詳細については調べきれていません。

まとめ

ちょっと前(といってもこの記事を最初に書いた時点(2020年11月)から1年ちょっとくらい前のことですが…)にScalaの並列コレクションを使ってプログラムを書いて(その際のTipsをこちらの記事にちょっとだけ書いています。)Linux上で実行してみたところ、CPUが持っている論理プロセッサをほぼすべてきっちり使い切ってくれて処理が爆速になっていろいろと捗ったので、Python3でも似たようなことができないかと考え、試してみた次第です。

今回はWindows10で試してみましたが、Linuxでも機会があれば試してみるかもしれません。

画像生成の処理は重い処理になることが多いので、処理のための処理時間を短縮することができると、その分try&errorを行うことのできる回数を増やせるのでかなりおすすめです。

この記事は以上です。

Related Posts / 関連ページ

【バージョンを変更しました。】SikuliX-2.0.1をインストールして、GIMP-2.10でよく使う操作を自動化してみた。 JavaのリストをScalaのリストに変換しようとしたところ、割と盛大にハマったのでメモ。 Windows 10 Homeでsbt-assemblyを使ってFat JARファイルを作ったところ、パスの文字列長が長すぎてクラスファイルが不足していて実行できなかった件。 Emacs 27.2をWindows 10のPCにインストールし、ついでにScalaの開発環境を再整備したり等してみた。