本Webサイトの記事を記事ごとにBag-of-Wordsモデルを使ってベクトル化してみた。

はじめに

機械学習の勉強を少しずつ始めています(厳密にはかなり久しぶりにおさらいをしています。)が、サンプルデータを使ったのでは、おもちゃで遊んでる感が否めない(※個人の感想です。)ので…

本Webサイトの記事で公開しているものを入力として、記事ごとにBag-of-Wordsモデルでベクトル化してみることにしました。

ベクトル化の前に形態素解析。

ベクトル化の対象となる特徴量は文書中に出現する単語の数ということになりますが…

単語の数を数えるには、数える対象となる単語が認識できていなければなりません。

英語の文書だと、

「単語はスペースで区切られているハズだから、そこで区切ればおk」

ということになりますが、スペースで単語の間を区切らない日本語の文書はそうはいきません。

そこで、形態素解析による品詞分解を行うのですが、この記事では話の成り行き上、以前作ったkuromojiを使ったテストプログラムをちょっと改造したものを使って品詞分解を行い、「記事ごとに現れる名詞の数」を抽出することにしました。

抽出結果は以下の例のようなJSONフォーマットの転置インデックスもどきとして出力しています。

{“人物”:[“5305,2″,”6890,20″],”Enable”:[“5776,1”]}

単語をキー、その直後にカンマ区切りの2個の整数の組(記事のIDと当該記事におけるキーの単語の出現回数(出現位置ではないことに注意です。)の組です。)を要素とする配列を値とする連想配列です。

ベクトル化します。

転置インデックスもどきができたら、それをBag-of-Wordsモデルを使ってベクトル化します。

ベクトル化といっても記事は複数ありますので、行数が記事の数に等しく、かつ列数がいずれかの記事に少なくとも1回出現する単語の数(以下、単に「単語数」と書きます。)に等しい行列の形式(この行列をとりあえず$A_0$と書くことにします。)で表すと、記述が少しばかり楽になるかもしれません。

また、1個の記事に登場する単語の数には限りがありそうですので、$A_0$の成分はほとんどが0、すなわち$A_0$は疎行列になりそうです。

そこで、$A_0$を読み込んでプログラム上に展開する際には、疎行列に特化した方法でメモリに格納したいところです。

Python3で以下のようなコードを書いてみます(import文は省略していますが、lil_matrixのimportが必要です)。なお、1行目の変数inputfileには前節の転置インデックスもどきのファイル名を指定します。

すると変数bowに$A_0$が読み込まれます。

上記のコードの先頭に適切なimport文を追加して実行すると、$A_0$の行数、列数及び0でない成分の個数が求まります。

C:\Users\pandanote\python3>python3 freqreadtest.py
261 8984 35061

記事の個数($m$)が261で単語数($n$)が8984であることから、$A_0$は261行8984列の行列であることがわかります。

また、0でない成分の個数が35061個ありますが、これは$A_0$の成分の総数($261 \times 8984 = 2344824$)の約1.495%に相当します。

すなわち、$A_0$は成分の約98.5%が0であることがわかります。

TF-IDFによる重要度の計算

文書における単語の重要度の求め方にはいくつかの手法が提案されていますが、この記事ではその中でも最も基本的な手法であるTF-IDFを用いて重要度を計算します。

なお、プログラミングの都合上、$A_0$の先頭行の行番号及び列番号は0としています。

単語の出現率による成分の正規化

本Webサイトの記事ごとの長さ(単語数)にはそれなりのばらつきがあるため、記事どうしの間の関係を調べるために利用することを想定し、$A_0$の$(i,j)$成分$a_{ij}$($0 \le i \lt m, 0 \le j \lt n$)を以下の(\ref{eq:tf})式で計算できる$a_{TF,ij}$に置き換えます。

\begin{align}
a_{TF,ij} &= \frac{a_{ij}}{\displaystyle\sum_{k=0}^{n-1}a_{ik}} \label{eq:tf}
\end{align}

$a_{TF,ij}$は文書$i$から抽出された単語の総単語数のうち、単語$j$の出現数の占める割合、すなわち出現頻度(TF: Term Frequency)を表すことになります。

以下、(\ref{eq:tf})式の計算により置き換えられた$a_{TF,ij}$を成分として持つ$m$行$n$列の行列を$A_{TF}$と書くことにします。

逆文書頻度による単語の重要度の調整

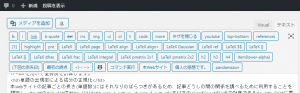
本Webサイトで使用しているWordpressのClassic Editor用のショートコードとしてh2タグなどのHTMLのセクションタグや$\LaTeX$の数式などだけでなく、一部の定型文についてもQuickTags APIを使ってテンプレート化してエディタの上側のボタンを押す(またはタップする)だけで挿入できるようになっています(下図参照。なお、追加の方法についてはこの記事をご参照ください)。

テンプレートに含まれる単語についてはほとんどの記事に登場する可能性がありますが、登場する記事の内容に常に深く関係しているかというと、必ずしもそうとは言えないと思います。

そこで、文書の総数$|D|$をある単語が出現する(同一文書内における出現回数は考慮しません。)文書の数$d_j (0 \le j \lt n)$で割った値を考えます(Wikipediaの記述とは$i$と$j$のnotationが入れ替わっていますが、気にしない方向でお願いします)。この値(以下、$\text{idf}_j$)を逆文書頻度(IDF: Inverse Document Frequency)といいます…

と言いたいところですが、ざっと調べた範囲では、

\begin{align}
\text{idf}_j &= \frac{|D|}{d_j} \label{eq:idfnormal} \cr
&= \log\frac{|D|}{d_j} \label{eq:idfloge} \cr
&= \log_{10}\frac{|D|}{d_j} \label{eq:idflogten}
\end{align}

の3通りの定義があるようです[1]。

どれを使ってもよいということになっているようですので、この記事では(\ref{eq:idfloge})式を採用することにします。

採用する式が決まったところで、(\ref{eq:idfloge})式で求められる$\text{idf}_j$を使って$A_{TF}$の$(i,j)$成分$a_{TF,ij}$($0 \le i \lt m, 0 \le j \lt n$)を以下の(\ref{eq:tf})式で計算できる$a_{TFIDF,ij}$に置き換えます。

$a_{TFIDF,ij}$の添え字の「TFIDF」は「TF-IDF」と書くべきところですが、TFからIDFを引く引き算と混同されるかもしれないので、中間の「-」は省いています。

\begin{align}
a_{TFIDF,ij} &= a_{TF,ij}\,\text{idf}_j \nonumber \cr
&= a_{TF,ij}\,\log\frac{|D|}{d_j} \label{eq:tfidf}
\end{align}

$a_{TFIDF,ij}$を成分として持つ$m$行$n$列の行列を$A_{TFIDF}$と書くことにします。

$A_{TFIDF}$がベクトル化の結果を表す行列になります。$\blacksquare$

コード例

本節のコード例は以下のような感じになります。

前半がTF、後半がIDFを求めるコードになります。変数bowに$A_0$をセットすると、変数aaに最終的に$A_{TFIDF}$が代入されます。

計算結果(の一部)の可視化

Seabornを用いた可視化

$A_{TFIDF}$の計算結果ですが、0でない成分の個数だけでもかなりの数になりますし、数字の羅列として表示してもいまいちイメージがつかみにくそうなので、視覚的にわかりやすい形で表現できないか考えます。

そうは言っても、$A_{TFIDF}$はかなり「横長な」行列になってしまいますので、行の数(261)に合わせて0列目から260列目までを切り出して261次の正方行列($A_{TFIDF}^{\prime}$)とし、それをSeabornでグラフとして描画し、とりあえず様子を見ることを考えます。

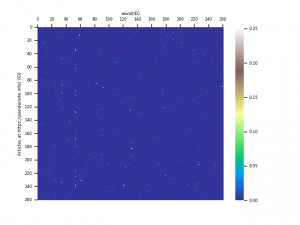
Seabornは設定すべき項目がかなりあって、見やすいグラフにするにはそれなりの熟練が必要ですが、めげずに設定すると…

…のような結果が得られます。カラーマップはterrainを使用しています。

ノイズっぽく点が見えるところが値が大きい成分を示します。また、青いところは対応する成分の値が0になっているところです。

$A_{TFIDF}^{\prime}$はほとんどの成分が0であることがわかります。

2次元より3次元

前節のグラフでは0の成分のところは青色で表示されていて、0以外の成分がホワイトノイズにしか見えない感じの画像になっていますが、0ではないものの値が小さいために薄めの青色で表示されている成分もまとめて0であるかのように見えてしまっているので、0でない成分が実際の比率よりも少なく見えている感じがします。

そこで…

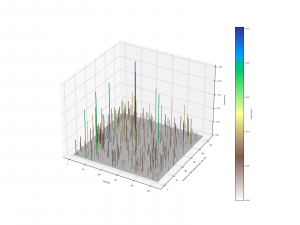
matplotlibの設定をちょっといじって、3次元表示にしてみました。

地面が青色になってしまうのを防ぐため、カラーマップはterrain_rを使用することで色の順序を上下逆にしています。

2次元のグラフよりは見やすくなったと思います。👍

まとめ

matplotlib及びseabornは初めて使いましたが、3次元表示にたどり着くまでがかなり大変でした。3次元表示にするまでに必要なコード例等については別の記事を立てて書くかもしれません。

seabornによる3次元表示のレンダリングは処理に時間がかかるようなので、データ点の数が増えてくると前節のグラフをmatplotlibのshow()メソッドで表示されるGUI上で操作することによっていろいろな角度から見るということが(描画処理が重くなってしまうせいか)簡単にはできなさそうなので、いろいろな角度から見てデータの状況を確認したい場合等には動画を作って確認する等の他の手段が必要かもしれません。

この記事は以上です。