住宅ローンの月々の返済額の概算にも使えるかもしれない複利計算での月々の返済額の計算式の導出。

はじめに

本Webサイトの管理人たるpandaは、現在住宅ローンを絶賛返済中であります。

毎月なんとなく返済している住宅ローンではありますが、月々の返済額の計算式ってどうやって求めたらいいのか考え始めると、心配で夜しか眠れなくなってしまいます。(´・ω・｀)

そこで、議論を簡単にするために適当な仮定を置きつつ、月々の返済額の計算式を導出してみることにしました。(｀・ω・´)

まず、適当な仮定を置きます。

前節で予告した通り、以下の適当な仮定を置くことします。

融資及び返済はともにちょうど1ヵ月ごとに行われるものとします。すなわち、資金の貸し出しから1回目の返済までの期間はちょうど1ヵ月であるとします。
1円未満の端数の処理方法については考えないことにします。
金利は全期間固定金利とします。すなわち、貸した側が金利上昇に伴うリスクを負うことになります(話が横道に逸れますが、変動金利は借りた側が金利上昇に伴うリスクを負うことになります。よって、融資を行う金融機関等は変動金利でローンを組むことを普通におすすめしてきます)。
月々の返済方法は元利均等返済でかつボーナス支給月などの増額返済は行わない、すなわち毎月の返済額は同一とします。これまた話が横道に逸れますが、ボーナスを返済計画に組み込むとボーナスからも金利を支払うことになりますので、ボーナスについては予備資金とし、時々繰り上げ返済するのがベターな選択です(※個人の意見です)。

導出していきます。

漸化式からの一般項。

まず1年あたりの金利(年利)を$\alpha^{\prime}$と置きます。なぜ、$\alpha$でなくて$\alpha^{\prime}$と置くのかといいますと、この後は1ヵ月あたりの金利(月利)で計算していくためにあまり出番がないからです。

月利をあらためて$\alpha$と置くと、$\alpha$及び$\alpha^{\prime}$の間には以下の(\ref{eq:yearandmonth})式が成り立ちます。

\begin{align}
1+\alpha &= (1+\alpha^{\prime})^{\frac{1}{12}}\label{eq:yearandmonth}
\end{align}

次に、借りた資金を$a_0$として、1回目の返済日以降1ヵ月ごとに$\beta$だけ返済し資金を借りてからちょうど$n$ヵ月後に完済するとします。$k$回目の返済直後の未返済の元金(残債)$a_k$は$k-1$回目の返済直後の残債$a_{k-1}$が月利の分だけ成長してから返済によって$\beta$だけ減った金額に等しいと考えることができますので、(\ref{eq:ak})式のように表すことができます。

\begin{align}
a_k &= (1+\alpha)a_{k-1}-\beta \label{eq:ak}
\end{align}

(\ref{eq:ak})式の両辺から$\displaystyle\frac{\beta}{\alpha}$を引くと…

\begin{align}
a_k – \frac{\beta}{\alpha} &= (1+\alpha)a_{k-1}-\beta-\frac{\beta}{\alpha}\nonumber\cr
&= (1+\alpha)a_{k-1} – \frac{\beta}{\alpha}(\alpha + 1)\nonumber\cr
&= (1+\alpha)(a_{k-1} – \frac{\beta}{\alpha}) \label{eq:recurrence}
\end{align}

となります。

(\ref{eq:recurrence})式はまぎれもない漸化式ですので…

\begin{align}
a_k – \frac{\beta}{\alpha} &= (1+\alpha)^k(a_0 – \frac{\beta}{\alpha})\nonumber\cr
a_k &= (1+\alpha)^k(a_0 – \frac{\beta}{\alpha})+\frac{\beta}{\alpha} \label{eq:aksolution}
\end{align}

となります。$a_0$は住宅ローンの借入金額を表します。

月々の返済額の概算額を求めます。

住宅ローンを借りてから$n$ヵ月後には住宅ローンが完済されますので、残債は0になるはずです。よって、(\ref{eq:aksolution})式より、

\begin{align}
a_n &= (1+\alpha)^n(a_0 – \frac{\beta}{\alpha})+\frac{\beta}{\alpha} \nonumber\cr
&=0\label{eq:anequation}
\end{align}

となりますので、月々の返済額$\beta$は

\begin{align}
&{} (1+\alpha)^n(a_0 – \frac{\beta}{\alpha})+\frac{\beta}{\alpha} = 0\label{eq:betaequation}
\end{align}

を$\beta$について解けば良いことになります。なお、(\ref{eq:betaequation})式の両辺に$\alpha$をかけて、

\begin{align}
(1+\alpha)^n(\alpha a_0 – \beta)+\beta &= 0\label{eq:betaequationmul}
\end{align}

としておくと考えやすいです。

(\ref{eq:betaequationmul})式より、

\begin{align}
\alpha a_0 (1+\alpha)^n &= \left[ (1+\alpha)^n -1 \right]\beta \nonumber\cr
\beta &= \frac{\alpha a_0 (1+\alpha)^n}{(1+\alpha)^n -1}\label{eq:betasolution}
\end{align}

となります。

(\ref{eq:betasolution})式の右辺の$a_0, \alpha, n$は既知の値ですので、$\beta$が計算できることになります。

計算例

2500万円を年利1.5%で借り入れて、35年(=420ヵ月)で返済するものとします。

この場合、$a_0 = 25000000, n = 420, \alpha^{\prime} = 0.015$となり、$\alpha$は(\ref{eq:yearandmonth})式より、

\begin{align}
\alpha &= (1+0.015)^{\frac{1}{12}}-1 \nonumber\cr
&= 0.00124148771 \cdots \label{eq:realalpha}
\end{align}

となりますので、(\ref{eq:betasolution})式より月々の返済額$\beta$は…

\begin{align}
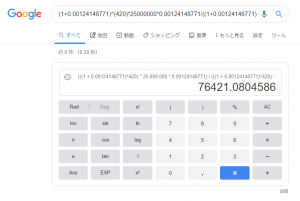
\beta &= \frac{25000000\cdot0.00124148771 \cdots \cdot(1+0.00124148771 \cdots)^{420}}{(1+0.00124148771 \cdots)^{420}-1} \nonumber\cr
&= 76421.0804586 \cdots \label{eq:realbeta}
\end{align}

と計算できます。月々の返済額は76421円くらいになります。😎

(\ref{eq:realbeta})式の計算には、Google先生の検索窓についている電卓機能を使いました↓

<br />

まとめ

ここまでの本Webサイトの数学系の記事と比較するとレベル感的にはかなり異なるものがあるかもしれませんが、複利でお金を借りた場合の月々の返済額の概算額の計算式の導出の方法について書いているところがあまり見当たらないような気もしたので、試しに導出してみました。

なお、この記事では融資や返済がちょうど1ヵ月ことに行われると仮定し、かつ月割で計算を行っていますので、実際の返済額とはわずかに異なることの方が多いと思います。これは、実際の住宅ローンなどの返済額の計算の際には月割(1/12)ではなく日割(28-31/365 or 366)で計算されることがあることや、1円未満の端数の処理や最終回の返済額の支払い額の計算方法等、細部が融資元の金融機関等ごとに異なることによるものです。

よって、実際の返済額の細部については融資元の金融機関にお問い合わせされることを強くお勧めいたします。

この記事は以上です。