第2種楕円積分の導出の方法がうろ覚えだと、いざというときにハマる件

はじめに

結論についてはWikipediaを見ていただくのが一番早いのですが、

「なんでそうなるんだっけ?」

などど考え始めて計算を進めると、計算の結果の式を見て焦ることになるので、メモっておくことにしました。

サクサクと計算

直截な導出法

最初に最も直截(と思われる)方法で以下の式にたどり着くことを考えます(Wikipediaに記載の式です)。

\begin{align}
E(\varphi, k) &= \int_0^{\varphi}\sqrt{1-k^2\sin^2\theta}\,d\theta \label{eq:secondellipticintegral}
\end{align}

まず、$xy$平面上の楕円

\begin{align}
\frac{x^2}{a^2}+\displaystyle\frac{y^2}{b^2} &= 1 \quad (a > b > 0) \label{eq:ellipse}
\end{align}

(下図参照)の周の長さを求めることを考えます。

なお、この楕円は$x$軸及び$y$軸に関して対称なので、$x \ge 0, y \ge 0$の部分(下図の青い実線の部分)だけ考えます。楕円の1周分の長さが必要であれば$x \ge 0, y \ge 0$の部分の弧の長さを求め、それを4倍すればよいという寸法です。

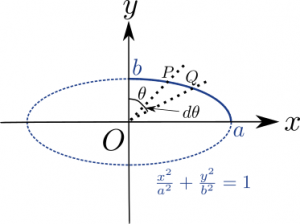
ここで、$y$軸の正の向きの半直線とのなす角(右回りを正とします。←ここ重要)が$\theta$であり、原点$O$を端点とする半直線を考え、それと楕円(\ref{eq:ellipse})の交点を$P$とします。

また、$y$軸の正の向きの半直線とのなす角が$\theta+d\theta$であり、原点$O$を端点とする半直線を考え、それと楕円(\ref{eq:ellipse})の交点を$Q$とします。

$P$,$Q$の位置関係を下図に示します。

すると、$P$の座標は$(a\sin\theta,b\cos\theta)$、$Q$の座標は$(a\sin(\theta+d\theta),b\cos(\theta+d\theta))$と表すことができます。

ここで、$d\theta$が$\theta$と比較して微小な正の数であるとし、微小な長さの線分$PQ$の長さ$|PQ|$を計算します。

すると…

\begin{align}
|PQ| &= \sqrt{a^2\{\sin(\theta+d\theta)-\sin\theta\}^2+b^2\{\cos(\theta+d\theta)-\cos\theta\}^2} \nonumber \\
&= \sqrt{a^2\{\sin\theta\cos d\theta+\cos\theta\sin d\theta-\sin\theta\}^2+b^2\{\cos\theta\cos d\theta-\sin\theta\sin d\theta-\cos\theta\}^2}\label{eq:dsfirst}
\end{align}

と表すことができます。

ここで、(\ref{eq:dsfirst})式を$d\theta$が微小であることに着目してさらに変形することを考えます。

$d\theta$は微小であるため、$\sin d\theta = d\theta, \cos d\theta = 1$であると考えます。

すると…

\begin{align}
|PQ| &= \sqrt{a^2\{\sin\theta+d\theta\cos\theta-\sin\theta\}^2+b^2\{\cos\theta-d\theta\sin\theta-\cos\theta\}^2} \nonumber \cr
&= \sqrt{a^2\{d\theta\cos\theta\}^2+b^2\{-d\theta\sin\theta\}^2} \nonumber \cr
&= \sqrt{a^2(d\theta)^2\cos^2\theta+b^2(d\theta)\sin^2\theta} \nonumber \cr
&= d\theta\sqrt{a^2\cos^2\theta+b^2\sin^2\theta} \nonumber \cr
&= d\theta\sqrt{a^2(1-\sin^2\theta)+b^2\sin^2\theta} \nonumber \cr
&= d\theta\sqrt{a^2+(b^2-a^2)\sin^2\theta} \nonumber \cr
&= d\theta\sqrt{a^2-(a^2-b^2)\sin^2\theta} \nonumber \\
&= a\,d\theta \sqrt{1-\frac{a^2-b^2}{a^2}\sin^2\theta} \label{eq:dssecond}
\end{align}

と計算できます。

(\ref{eq:dssecond})式の最後だけいまいちシンプルな式でない感じもしますが、$a$は楕円の長半径であり、$b$は短半径であるので、離心率$k$($e$と書くこともありますが、ここでは(\ref{eq:secondellipticintegral})式と合わせて$k$と書きます。)を

\begin{align}
k = \sqrt{\frac{a^2-b^2}{a^2}} \label{eq:eccentricity}
\end{align}

で表すことができます。

よって、(\ref{eq:eccentricity})式を(\ref{eq:dssecond})式に代入すると…

\begin{align}
|PQ| &= a\,d\theta\sqrt{1-k^2\sin^2\theta} \label{eq:dsthird}
\end{align}

と表すことができます。

ここで、楕円(\ref{eq:ellipse})と$y$軸の正の向きとの交点を$P_0$、原点$O$を端点とする半直線を考え、それと楕円(\ref{eq:ellipse})の交点を$P_{\varphi}$としたときに、その半直線と$y$軸の正の向きとのなす角を$\varphi$とします。

この時、弧$P_0P_{\varphi}$は(\ref{eq:dsthird})式で求めることのできる微小な線分$|PQ|$をつなぎ合わせたものの総和であると考えることができるので、弧$P_0P_{\varphi}$の長さ$|P_0P_{\varphi}|$は$|PQ|=ds$とおくと…

\begin{align}
|P_0P_{\varphi}| &= \int_{P_0P_{\varphi}}ds \nonumber \cr
&= \int_{0}^{\varphi}a\sqrt{1-k^2\sin^2\theta}\,d\theta \nonumber \cr
&= a\int_{0}^{\varphi}\sqrt{1-k^2\sin^2\theta}\,d\theta \nonumber \\
&= a\,E(\varphi, k) \label{eq:dsfinal}
\end{align}

と表すことができます。

(\ref{eq:dsfinal})式で$a=1$とおくと、(\ref{eq:secondellipticintegral})式が現れます。$\blacksquare$

ハマりがちな導出法

ところが、大学の受験勉強の時代からの癖で

「えっと、動径は左回りが正だから、っと…」

と考えて、下図のように点Pの座標を$(a\cos\theta,b\sin\theta)$、点Qの座標を$(a\cos(\theta+d\theta),b\sin(\theta+d\theta))$ととったとします。

すると、$|PQ|$は…

\begin{align}
|PQ| &= \sqrt{a^2\{\cos(\theta+d\theta)-\cos\theta\}^2+b^2\{\sin(\theta+d\theta)-\sin\theta\}^2} \nonumber \cr
&= \sqrt{a^2\{\cos\theta\cos d\theta-\sin\theta\sin d\theta-\cos\theta\}^2+b^2\{\sin\theta\cos d\theta+\cos\theta\sin d\theta-\sin\theta\}^2} \nonumber \cr
&= \sqrt{a^2\{\cos\theta-d\theta\sin\theta-\cos\theta\}^2+b^2\{\sin\theta+d\theta\cos\theta-\sin\theta\}^2} \nonumber \cr
&= \sqrt{a^2\{-d\theta\sin\theta\}^2+b^2\{d\theta\cos\theta\}^2} \nonumber \cr
&= \sqrt{a^2(d\theta)^2\sin^2\theta+b^2(d\theta)\cos^2\theta} \nonumber \cr
&= d\theta\sqrt{a^2\sin^2\theta+b^2\cos^2\theta} \nonumber \cr
&= d\theta\sqrt{a^2(1-\cos^2\theta)+b^2\cos^2\theta} \nonumber \cr
&= d\theta\sqrt{a^2+(b^2-a^2)\cos^2\theta} \nonumber \cr
&= d\theta\sqrt{a^2-(a^2-b^2)\cos^2\theta} \nonumber \cr
&= a\,d\theta\sqrt{1-\frac{a^2-b^2}{a^2}\cos^2\theta} \nonumber \\
&= a\,d\theta\sqrt{1-k^2\cos^2\theta} \label{eq:dscosfirst}
\end{align}

と表すことができます。

(\ref{eq:secondellipticintegral})式とは微妙に式が異なりますが、それものそのはず、積分の経路を楕円の弧上において逆向きにとっていることに起因する相違です。

とりあえずこの相違は置いておいて、$E(\cdot)$を用いた形で表すことができないか考えてみます。

(\ref{eq:dsfinal})式を計算した時と同様に$x$軸上に$P_0$、楕円の円弧上に$P_{\psi}$をとることにすると…

\begin{align}
|P_0P_{\psi}| &= \int_{P_0P_{\varphi}}ds \nonumber \cr
&= \int_{0}^{\psi}a\sqrt{1-k^2\cos^2\theta}\,d\theta \nonumber \\
&= a\int_{0}^{\psi}\sqrt{1-k^2\cos^2\theta}\,d\theta \label{eq:dscosthird}
\end{align}

と表すことができます。

ここで、$\psi \in \left[ 0, \displaystyle\frac{\pi}{2} \right]$であることに着目し、$t = \displaystyle\frac{\pi}{2} – \theta$とおいて(\ref{eq:dscosthird})式に代入すると…

\begin{align}
a\int_{0}^{\psi}\sqrt{1-k^2\cos^2\theta}\,d\theta &= -a\int_{\frac{\pi}{2}}^{\frac{\pi}{2}-\psi}\sqrt{1-k^2\sin^2t}\,dt \nonumber \cr
&= a\int_{\frac{\pi}{2}-\psi}^{\frac{\pi}{2}}\sqrt{1-k^2\sin^2t}\,dt \nonumber \cr
&= a\left(\int_{0}^{\frac{\pi}{2}}\sqrt{1-k^2\sin^2t}\,dt\,\, – \int_{0}^{\frac{\pi}{2}-\psi}\sqrt{1-k^2\sin^2t}\,dt\right) \nonumber \\
&= a\left(E\left(\frac{\pi}{2},k\right)-E\left(\frac{\pi}{2}-\psi,k\right)\right) \label{eq:dscosfinal}
\end{align}

…と$E(\cdot)$を用いた形で表すことができます。$\blacksquare$

まとめ

$E(\cdot)$を用いた形で表すことはできるのですが、ちょっと回りくどくて、かつ直感的にはいまいちわかりにくい式になってしまう点については、第2種楕円積分の式を(\ref{eq:secondellipticintegral})式の形式($\sin$が現れる形式)として定義してしまった先人の中の人を恨むより他はありません。

第2種楕円積分は楕円(または楕円の弧)の周の長さを求めるときに現れます。

円(または円弧)の周の長さを求める式と比較しても複雑さが段違いであることがおわかりいただけるかと思います。

この記事は以上です。