ディリクレ積分をフーリエ変換を使って計算しようとしたらいろいろと出てきたので、まとめてメモ。

はじめに

ディリクレ積分

\begin{align}
\int_{0}^{\infty} \frac{\sin x}{x} dx &= \displaystyle\frac{\pi}{2} \label{eq:dirichletint}
\end{align}

を証明する方法は複素積分を使う方法をはじめとしていろいろあります。

それ以外の方法はないかと、いろいろと調べて回っているうちにどこかで見かけたフーリエ変換を使う方法が面白そうだなと思ったまま、そのURLを失念してしまったので、自力で計算してみることにしました。

計算をするにあたり、関連する情報がいろいろと出てきたので、ついでにメモしておきます。

さっそく、計算してみます。

矩形関数のフーリエ変換

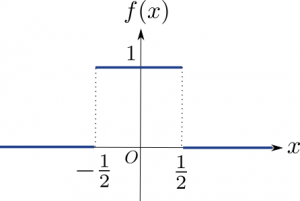
というわけで、かなり唐突かもしれませんが、(\ref{eq:squarewave})式のような関数を考えます。

\begin{align}
f(x) &= \left\{
\begin{array}{l}
1 & \left(|x| \le \displaystyle\frac{1}{2}\right) \cr
0 & \left(|x| \gt \displaystyle\frac{1}{2}\right)
\end{array}
\right. \label{eq:squarewave}
\end{align}

以下のようなグラフになります。矩形波1個分です。🙂

(\ref{eq:squarewave})式で表される関数$f(x)$は$\bigg(|x| = \displaystyle\frac{1}{2}$で不連続ですが、$\bigg)$絶対可積分であり、

\begin{align}
\int_{-\infty}^{\infty} |f(x)|dx &= 1 \lt \infty \label{eq:squarewavearea}
\end{align}

となります。

そこで、フーリエ変換$F(\xi)$を計算してみる(間違えやすいところなので、あまり省略しないで計算します。)と…

\begin{align}
F(\xi) = \int_{-\infty}^{\infty} f(x) e^{-2\pi x\xi i} dx &= \int_{-\frac{1}{2}}^{\frac{1}{2}} e^{-2\pi x\xi i} dx \nonumber \cr
&= \left[ \frac{e^{-2\pi x\xi i}}{-2\pi\xi i} \right]_{-\frac{1}{2}}^{\frac{1}{2}} \nonumber \cr
&= \frac{e^{-\pi \xi i} – e^{\pi \xi i}}{-2\pi\xi i} \nonumber \cr
&= \frac{\cos\pi \xi-i\sin\pi\xi – \cos\pi\xi -i\sin\pi\xi}{-2\pi\xi i} \nonumber \cr
&= \frac{2i\sin\pi\xi}{2\pi\xi i} \nonumber \cr
&= \frac{\sin\pi\xi}{\pi\xi} \label{eq:fouriertransform}
\end{align}

と計算できます。

逆変換してみます。

次に、$F(\xi)$のフーリエ逆変換を考えます。

$F(\xi)$のフーリエ逆変換$f(x)$は(\ref{eq:fourierinverse})式で表されます。

\begin{align}
f(x) &= \int_{-\infty}^{\infty} F(\xi)e^{2\pi\xi xi} d\xi \nonumber \cr
&= \int_{-\infty}^{\infty} \frac{\sin\pi\xi}{\pi\xi}e^{2\pi\xi xi} d\xi \label{eq:fourierinverse}
\end{align}

ここでフーリエ逆変換を計算する前に、(\ref{eq:fourierinverse})式は$\xi$についての積分であることに注意しつつ、$x=0$を代入してみます。

すると、(\ref{eq:squarewave})式より

\begin{align}
f(0) &= \int_{-\infty}^{\infty} \frac{\sin\pi\xi}{\pi\xi} d\xi \nonumber \cr
&= 1 \label{eq:fourierinverseatzero}
\end{align}

となることがわかります。

そこで、$t = \pi\xi$とおくと、

\begin{align}
\int_{-\infty}^{\infty} \frac{\sin\pi\xi}{\pi\xi} d\xi &= \int_{-\infty}^{\infty} \frac{1}{\pi}\cdot\frac{\sin t}{t} dt
= 1 \label{eq:ftparamtrans}
\end{align}

(\ref{eq:ftparamtrans})式の右側2辺を$\pi$で割って積分の変数$t$を$x$に置き換えると、

\begin{align}
\int_{-\infty}^{\infty} \frac{\sin x}{x} dx
&= \pi \label{eq:doubleddirichletint}
\end{align}

となります。

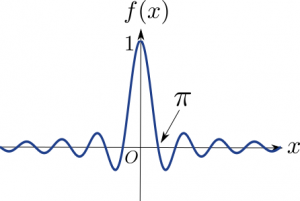
なお、$f(x) = \displaystyle\frac{\sin x}{x}$のグラフは以下のような感じになります。

また、$\displaystyle\frac{\sin x}{x}$は偶関数であるため、

\begin{align}
\int_{0}^{\infty} \frac{\sin x}{x} dx
&= \frac{\pi}{2}
\end{align}

となります。

以上で、(\ref{eq:dirichletint})式を示すことができました。$\qquad\blacksquare$

ここからが本当のフーリエ逆変換です。

ここで、$F(\xi)$のフーリエ逆変換が$f(x)$になることもついでに確認してみます。

(\ref{eq:doubleddirichletint})式を利用しつつ、(\ref{eq:fourierinverse})式の右辺を計算します。

\begin{align}
\int_{-\infty}^{\infty} \frac{\sin\pi\xi}{\pi\xi}e^{2\pi\xi xi} d\xi &= \int_{-\infty}^{\infty} \frac{\sin\pi\xi}{\pi\xi}(\cos 2\pi\xi x+i\sin 2\pi\xi x) d\xi \label{eq:fourierinversetriangle}
\end{align}

ここで、$g(\xi) = \displaystyle\frac{\sin\pi\xi\sin 2\pi\xi x}{\pi\xi}$と置くと、$g(-\xi) = g(\xi)$ですので、$g(\xi)$は奇関数であることがわかります。したがって(\ref{eq:fourierinversetriangle})式の右辺の虚数部は0であることがわかるので、

\begin{align}
\int_{-\infty}^{\infty} \frac{\sin\pi\xi}{\pi\xi}(\cos 2\pi\xi x+i\sin2\pi\xi x) d\xi &= \int_{-\infty}^{\infty} \frac{\sin\pi\xi}{\pi\xi}\cos 2\pi\xi x d\xi \nonumber \cr
&= \int_{-\infty}^{\infty} \frac{1}{2\pi\xi}[\sin\pi\xi(1+2x)+\sin\pi\xi(1-2x)] d\xi
\label{eq:fourierinversedirichlet}
\end{align}

となります。(\ref{eq:fourierinverseatzero})式と似た式が現れました。ただ、$\sin$の中のうち積分変数$\xi$を除く部分の値が$x$の値によっては負の値になるケースがありそうです。

(\ref{eq:fourierinverseatzero})式を少しだけ一般化して、$h(\alpha) = \displaystyle\int_{-\infty}^{\infty} \displaystyle\frac{\sin \alpha \xi}{\alpha \xi}d\xi \,(\alpha \ne 0)$と置くと、$\alpha$が負の値の場合には符号が反転しますので、$\alpha$が正の場合と合わせて

\begin{align}
\int_{-\infty}^{\infty} \frac{\sin \alpha \xi}{\alpha \xi}d\xi &= \frac{\pi}{\alpha{\rm sgn}(\alpha)} \label{eq:sincintegral}
\end{align}

と表すことができます。ただし、${\rm sgn}(x)$は符号関数

\begin{align}
{\rm sgn}(x) &= \left\{
\begin{array}{l}
1 & \left(x \gt 0\right) \cr
0 & \left(x = 0\right) \cr
-1 & \left(x \lt 0\right) \cr
\end{array}
\right. \label{eq:signfunction}
\end{align}

を表します。

(\ref{eq:sincintegral})式右辺の分母は$|\alpha|$と書いてもいいのですが、後の計算の都合があるので、このような形で表しておきます。

ここで本題に戻りまして、(\ref{eq:sincintegral})式を利用しつつ(\ref{eq:fourierinversedirichlet})式の右辺第1項の積分を計算します。$x = -\displaystyle\frac{1}{2}$のときのことはいったん忘れて、$x \ne -\displaystyle\frac{1}{2}$として以下のように変形できます。

\begin{align}
\int_{-\infty}^{\infty} \frac{1}{2\pi\xi}\sin\pi\xi(1+2x) d\xi &= \int_{-\infty}^{\infty} \frac{1+2x}{2}\cdot\frac{\sin\pi\xi(1+2x)}{\pi\xi(1+2x)} d\xi \nonumber \cr
&= \frac{1+2x}{2}\int_{-\infty}^{\infty} \frac{\sin\pi\xi(1+2x)}{\pi\xi(1+2x)} d\xi \nonumber \cr
&= \frac{1+2x}{2}\cdot\frac{\pi}{\pi(1+2x){\rm sgn}(1+2x)} \nonumber \cr
&= \frac{1}{2{\rm sgn}(1+2x)} \nonumber \cr
&= \frac{{\rm sgn}(1+2x)}{2} \label{eq:fourierinverseatfirstsection}
\end{align}

最後の2行については${\rm sgn}(x)$が符号関数であることから、$\displaystyle\frac{1}{{\rm sgn}(x)} = {\rm sgn}(x)$であることを利用しています。

なお、変形の途中で$\pi(1+2x)$を(\ref{eq:sincintegral})式における$\alpha$だと思って計算しています。また$x = -\displaystyle\frac{1}{2}$のときには(\ref{eq:fourierinversedirichlet})式の右辺第1項の分子が0になりますので、積分した結果も0になります。これらをまとめると、

\begin{align}
\int_{-\infty}^{\infty} \frac{1}{2\pi\xi}\sin\pi\xi(1+2x) d\xi &= \left\{
\begin{array}{l}
\displaystyle\frac{{\rm sgn}(1+2x)}{2} & \left(x \ne -\displaystyle\frac{1}{2}\right) \cr
0 & \left(x = -\displaystyle\frac{1}{2}\right)
\end{array}
\right. \label{eq:fourierinverseatfirstsectionfinal}
\end{align}

となります。

(\ref{eq:fourierinversedirichlet})式の右辺第2項についても同様の議論ができて、

\begin{align}
\int_{-\infty}^{\infty} \frac{1}{2\pi\xi}\sin\pi\xi(1-2x) d\xi &= \left\{
\begin{array}{l}
\displaystyle\frac{{\rm sgn}(1-2x)}{2} & \left(x \ne \displaystyle\frac{1}{2}\right) \cr
0 & \left(x = \displaystyle\frac{1}{2}\right)
\end{array}
\right. \label{eq:fourierinverseatsecondsectionfinal}
\end{align}

となりますので、(\ref{eq:fourierinverseatfirstsectionfinal})式及び(\ref{eq:fourierinverseatsecondsectionfinal})式を足し合わせると、

\begin{align}
f(x) &= \left\{
\begin{array}{l}
1 & \left(|x| \lt \displaystyle\frac{1}{2}\right) \cr
\!\displaystyle\frac{1}{2} & \left(|x| = \displaystyle\frac{1}{2}\right) \cr
0 & \left(|x| \gt \displaystyle\frac{1}{2}\right) \cr
\end{array}
\right. \label{eq:fourierinversefinal}
\end{align}

となります。

元の関数が再び現れましたね。$\qquad\blacksquare$

$|x| = \displaystyle\frac{1}{2}$のところについてはフーリエ逆変換の結果が右極限と左極限の平均値になっていますが、気にしない方向でお願いいたします。😁

以下、余談が続きます。

ディリクレ関数

何かとディリクレ積分と間違えられやすいディリクレ関数ですが、ディリクレ関数は「すべての実数で定義される有理数の時に1、無理数の時に0をとる関数」で、(\ref{eq:dirichletfunction})式で表されます。

\begin{align}
f(x) &= \lim_{n \to \infty}\lim_{k \to \infty}\cos^{2k}(n!\pi x) \label{eq:dirichletfunction}
\end{align}

詳細な解説については参考文献に示したURLまたはWikipediaをご参照いただければと思います。

定義がわかりやすかったり、整数の階乗を有理数を選び出すために使ったりしているところは非常に面白いと思うのですが、どのように応用したらよいかがよくわからない関数ではあります。🐼

ディリクレ積分が絶対可積分でないことの証明

次に、ディリクレ積分は絶対可積分でないこと、すなわち、

\begin{align}
\int_{-\infty}^{\infty} \left|\frac{\sin x}{x}\right| dx &\to \infty \label{eq:dirichletinfty}
\end{align}

であることを証明してみます。

$\displaystyle\frac{\sin x}{x}$は偶関数なので、

\begin{align}
\int_{-\infty}^{\infty} \left|\frac{\sin x}{x}\right| dx &= 2\int_{0}^{\infty} \left|\frac{\sin x}{x}\right|dx\nonumber \cr
&= 2\sum_{n=0}^{\infty}\int_{n\pi}^{(n+1)\pi} \left|\frac{\sin x}{x}\right|dx\nonumber \cr
&= 2\sum_{n=0}^{\infty}\left(\int_{2n\pi}^{(2n+1)\pi} \frac{\sin x}{x}-\int_{(2n+1)\pi}^{(2n+2)\pi} \frac{\sin x}{x}\right)dx\nonumber \cr
&\gt 2\sum_{n=0}^{\infty}\left(\int_{2n\pi}^{(2n+1)\pi} \frac{\sin x}{(2n+1)\pi}-\int_{(2n+1)\pi}^{(2n+2)\pi} \frac{\sin x}{(2n+2)\pi}\right)dx\nonumber \cr
&= 2\sum_{n=0}^{\infty}\left(\frac{2}{(2n+1)\pi}+\frac{2}{(2n+2)\pi}\right) \nonumber \cr
&= 2\sum_{n=0}^{\infty}\frac{2}{(n+1)\pi}\nonumber \cr
&= 4\sum_{n=1}^{\infty}\frac{1}{n\pi}\label{eq:sumathalf}
\end{align}

と変形できますが、(\ref{eq:sumathalf})式の右辺は発散してしまいます。よって、(\ref{eq:dirichletinfty})式が成り立つこと、すなわち、絶対可積分ではないことが示されました。$\qquad\blacksquare$

Wikipediaには$\displaystyle\frac{\sin x}{x}$のフーリエ変換は矩形関数になることがしれっと書いてありますが、この記事ではそれが可能であるかどうかの議論には立ち入らず、$\displaystyle\frac{\sin x}{x}$のフーリエ逆変換のみを考えることとしています。