Inkscape(0.92.4)で積分経路を書いてから始める複素積分。

はじめに

前の記事では複素積分を使わないで、ディリクレ積分

\begin{align}
\int_{0}^{\infty} \frac{\sin x}{x} dx &= \frac{\pi}{2} \label{eq:dirchletintegral}
\end{align}

を計算しました。

この記事では、(\ref{eq:dirchletintegral})式を複素積分で計算する前に、積分経路をInkscapeでサクっと描くための手順について書いていきます。

ついでに、複素積分の計算も行います。🐼

また、「まとめ」の節におまけについての記述がありますので、ご覧いただけると幸いです。

Inkscapeで積分経路を描きます。

経路の描画

まず、複素積分を行う経路を複素平面上に以下の手順で描きます。

Inkscapeを起動します。
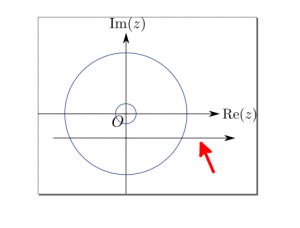
複素平面を描きます。実軸及び虚軸ならびに対応するラベルを描きます。ラベルは$\LaTeX$でレンダリングしたものを入れておきます。以下のような感じの図になります。
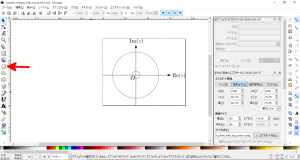
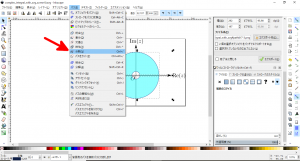
Inkscapeの「円/弧ツール」(下図の赤矢印)を使って、複素平面上で原点を中心とする円を2個描きます。なお、円の色や線の太さはお好みで調整します。
実軸をマウスの左クリック(以下、単に「左クリック」と書きます。)で選択後、メニューバーから「編集」→「コピー」と選択(またはCtrl-C)で実軸をコピーし、メニューバーから「編集」→「貼り付け」と選択(またはCtrl-V)して実軸を貼り付けます(下図の赤矢印)。
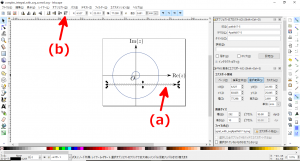
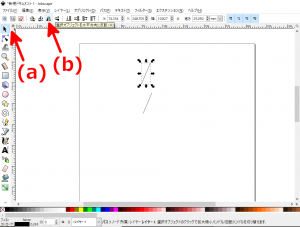
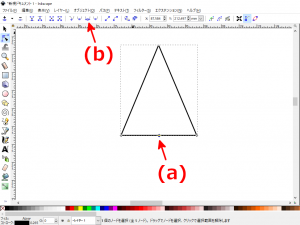
手順5で貼り付けた実軸(のコピー)を左クリックで選択(下図の赤矢印(a))後、ツールバーの「最前面に移動」(下図の赤矢印(b))をクリックし、実軸(のコピー)を最前面に移動させます。
実軸(のコピー)をコピー元の実軸の位置に移動します。
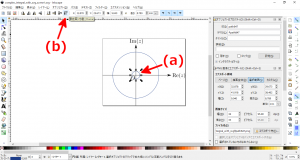
手順3で描いた2個の円のうち、内側の円を左クリックで選択(下図の赤矢印(a))後、ツールバーの「最前面に移動」(下図の赤矢印(b))をクリックし、最前面に移動させます。
Shiftキーを押しながら外側の円(下図の赤矢印)をクリックし、2個の円が両方とも選択した状態とします(下図)。
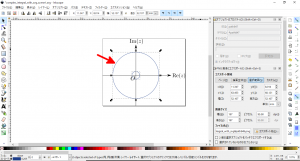
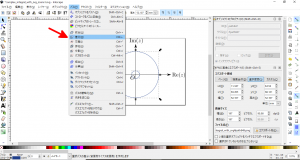
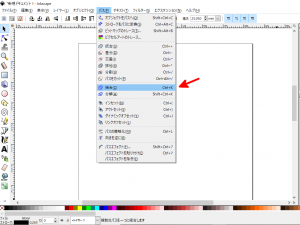
メニューバーから「パス」→「差分」(下図の赤矢印)と選択し、外側の円のオブジェクトの領域から内側の円のオブジェクトの領域を除外します。
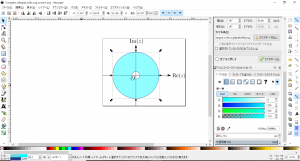
「フィル」が設定されていない場合には、試しに外側の円を選択して「フィル」に適当な色を設定し、内側の円の内側が領域から除外されていることを確認します。確認例を下図に示します。座標軸が隠れてしまうのを防ぐために指定した領域の色に$\alpha$値を設定しています。
手順9で作成した円筒型の領域を左クリックで選択後に実軸のコピーをShift+左クリックで選択します。
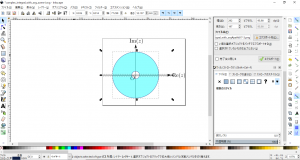
メニューバーから「パス」→「分割」と選択し、手順10で選択した領域を2分割します。
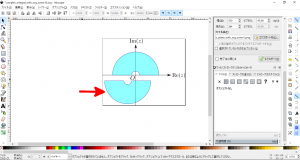
以下のような感じに切れます。なかなか爽快です。(｀・ω・´)
ただし、以下の図は手順12を実行後に、領域の下半分(下図の赤矢印)を左クリックで選択してドラッグすることで移動した後の画面であり、手順12を実行後にただちに以下の図のような表示にはなりません。
領域の下半分(下図の赤矢印)は不要なので、削除します。

鏃の自作

次にパスに対して矢印を設定… と思ったのですが、ちょっと調べた感じでは積分経路上にいい感じでセットできる鏃がなさそうだったので、以下の手順で自作することにしました。

Inkscapeを起動します。
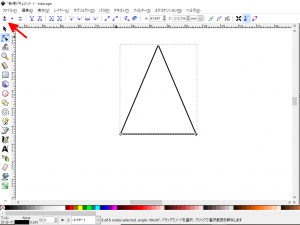
「ペンツール」で直線を引きます。
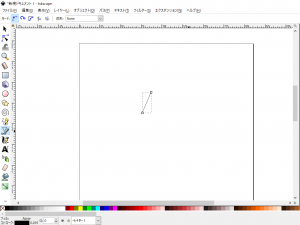
手順2で引いた直線をコピーして貼り付けます。
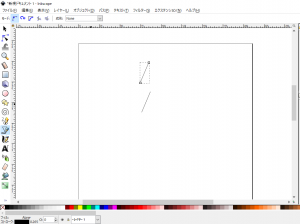
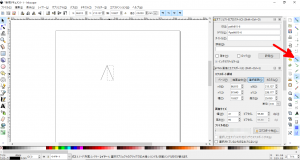
「選択ツール」のアイコン(下図の赤矢印(a))をクリックして選択ツールによる選択に切り替えると、ツールバーの表示が下図のように切り替わるので、「選択オブジェクトを水平方向に反転」(下図の赤矢印(b))を選択します。
「ノード、パス、およびハンドルをスナップ」が有効になっていることを確認後、手順4で反転したオブジェクトの端点のうち一方が元のオブジェクトの端点の一方と重なるように移動します。
2個のオブジェクトを選択し、メニューバーから「パス」→「結合」を選択します。すると、2個のオブジェクトが結合されます。
「ペンツール」で二等辺三角形の底辺にあたる部分の直線を引きます。
手順6で結合したオブジェクトと手順7で引いた直線を選択し、メニューバーから「パス」→「結合」を選択します。すると、2個のオブジェクトが結合されます。
二等辺三角形の底辺の両端の頂点が結合されているかどうかを確認します。結合されていない場合には、1つの頂点にノードの端点が2つ以上重なって存在していますので、以下の手順でノードの端点を1つにまとめます。
1. 「ノードツール」のアイコンをクリックしてから結合されていない頂点の周囲をマウスの左ボタンをクリックしてからドラッグすることで選択します。
2. ツールバーの「選択した端点ノードを連結」ボタン(下図の赤矢印)を押します。
「ノードツール」のアイコンをクリックしてから二等辺三角形の底辺を左クリックして選択します。
メニューバーの「新規ノードを選択セグメントに挿入」のアイコン(下図の赤矢印)をクリックします。
二等辺三角形の底辺の中点あたりに新しいノードが挿入されますので、そのノード(下図の赤矢印(a))を左クリックで選択後、メニューバーの「選択ノードの種類を対象に」アイコン(下図の赤矢印(b))をクリックします。
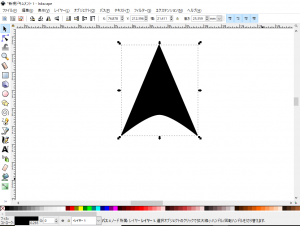
手順12で選択したノードを左クリックしてドラッグすると、そのノードを通る曲線を描くことができますので、鏃としていい感じになりそうな位置にノードを移動します。
お好みで「フィル」で鏃の内側の色を設定します。
SVGフォーマットのファイルとして保存します。

経路の向きを示す鏃の追加

鏃のSVGファイルが作成できたところで、それを経路を示す図に追加します。

SVGファイルはInkscapeのメニューバーから「ファイル」→「インポート」と選択し、鏃のSVGファイルを選択すると追加できます(下図)。

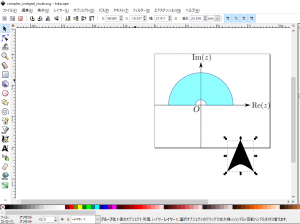
鏃を追加した直後は上図のような感じになってしまいますが、縮小しても表示が乱れることのないSVGフォーマットの利点を生かして、追加した鏃のサイズを変更して大きさを取りあえず決め、さらに回転及びその他の操作を繰り返します。

すると、以下のような感じに鏃を追加することができます。

あとは例によってお好みで記号等を以下のように追加すると積分経路を示した図の完成です。🐼

複素積分を計算します。

積分経路の図が書けたら、(\ref{eq:dirchletintegral})式となることを複素積分を利用して示します。

なお、この記事ではジョルダンの補題については証明無しで利用します。

まず、$f(z) = \displaystyle\frac{e^{iz}}{z}$と置くと、ここまでに描いてきた積分経路が囲む領域内には$f(z)$についての特異点は存在しないことから、(\ref{eq:noresidue})式が成り立ちます。

\begin{align}
\left( \int_{C_1} + \int_{C_2} + \int_{C_3} + \int_{C_4} \right) f(z)dz &= 0 \label{eq:noresidue}
\end{align}

ここで、経路$C_1$及び$C_3$は実軸上の経路、$C_2$は半径$R$の半円上の経路、$C_4$は半径$r$の半円上の経路を表すものとします。

$C_1$及び$C_3$は実軸上の経路なので、積分変数$z$は$x (\in {\mathbb R})$に置き換えることができて、

\begin{align}
\left( \int_{C_1} + \int_{C_3} \right) f(z)dz &= \int_{r}^{R} \frac{e^{ix}}{x} dx + \int_{-R}^{-r} \frac{e^{ix}}{x}dx \label{eq:onrealaxis}
\end{align}

(\ref{eq:onrealaxis})式右辺第2項の積分変数$x$を$x = -t$と置くと、

\begin{align}
\int_{-R}^{-r} \frac{e^{ix}}{x}dx &= \int_{R}^{r} \frac{e^{-it}}{-t}(-dt) \nonumber \cr
&= -\int_{r}^{R} \frac{e^{-it}}{t}dt \label{eq:dxdt}
\end{align}

となりますので、積分変数$t$を$x$に再度置き換えてから(\ref{eq:dxdt})式右辺を(\ref{eq:onrealaxis})式に代入すると、

\begin{align}
\left( \int_{C_1} + \int_{C_3} \right) f(z)dz &= \int_{r}^{R} \frac{e^{ix}}{x} dx -\int_{r}^{R} \frac{e^{-ix}}{x}dx \nonumber \cr
&= \int_{r}^{R} \frac{e^{ix}-e^{-ix}}{x}dx \nonumber \cr
&= 2i\int_{r}^{R} \frac{\sin x}{x}dx \label{eq:sincintonrealaxis}
\end{align}

となります。(\ref{eq:dirchletintegral})式と似た式が現れました。

また、$C_2$は$g(z)=\displaystyle\frac{1}{z}$と置くと、$f(z) = e^{iz}g(x)$という形で書けて、かつ$|z| \to \infty$のときに$g(z)$が複素平面上で一様に収束するので、ジョルダンの補題を使うことができて、

\begin{align}
\int_{C_2} f(z)dz &\to 0 \,\,(R \to \infty) \label{eq:withjordanlemma}
\end{align}

となります。

最後に、経路$C_4$に沿った積分について考えます。
$f(z)$を$z=0$のまわりでテイラー展開すると、

\begin{align}
\frac{e^{iz}}{z} &= \frac{1}{z}\sum_{n=0}^{\infty}\frac{(iz)^n}{n!}\nonumber\cr
&= \frac{1}{z}+\sum_{n=1}^{\infty}\frac{i^nz^{n-1}}{n!}\nonumber\cr
&= \frac{1}{z}+\sum_{n=0}^{\infty}\frac{i^{n+1}z^n}{n!}\label{eq:cfourtaylor}
\end{align}

となります。

ここで$z=re^{i\theta}$と置きます。$dz=ire^{i\theta}d\theta$となることと、積分変数$\theta$についての$\pi$から$0$までの積分となることに留意しつつ(\ref{eq:cfourtaylor})式の右辺第1項を計算します。

すると…

\begin{align}
\int_{C_4} \frac{1}{z} dz &= \int_{\pi}^{0} \frac{1}{re^{i\theta}}ire^{i\theta}d\theta \nonumber \cr
&= \int_{\pi}^{0}id\theta \nonumber \cr
&= \left[ i\theta \right]_{\pi}^{0} \nonumber \cr
&= -i\pi \label{eq:cfourfirstterm}
\end{align}

と計算でき、$r$に依存しない値となることがわかります。また、(\ref{eq:cfourtaylor})式の右辺第2項は、和と積分の順序を入れ替えることができるので、

\begin{align}
\int_{C_4} \sum_{n=0}^{\infty}\frac{i^{n+1}z^n}{n!} dz &= \int_{\pi}^{0} \sum_{n=0}^{\infty}\frac{i^{n+1}r^ne^{in\theta}}{n!}ire^{i\theta}d\theta \nonumber \cr
&= \int_{\pi}^{0} \sum_{n=0}^{\infty}\frac{i^nr^{n+1}e^{i(n+1)\theta}}{n!}d\theta \nonumber \cr
&= \sum_{n=0}^{\infty} \frac{i^nr^{n+1}}{n!}\int_{\pi}^{0}e^{i(n+1)\theta}d\theta \label{eq:cfoursecondterm}
\end{align}

と変形できて、和の各項に$r$のべき乗が現れるので、$r \to 0$とすると、各項がすべて$0$となります。
(\ref{eq:sincintonrealaxis}),(\ref{eq:withjordanlemma}),(\ref{eq:cfourfirstterm})及び(\ref{eq:cfoursecondterm})式を(\ref{eq:noresidue})式に代入し、$R \to \infty, r \to 0$とすると、

\begin{align}
\int_{0}^{\infty} 2i\frac{\sin x}{x}dx \,- \,i\pi &= 0 \label{eq:putvalues}
\end{align}

となるので、(\ref{eq:putvalues})式の左辺第2項を右辺に移項後に、両辺を$2i$で割ると、$\displaystyle\int_{0}^{\infty} \displaystyle\frac{\sin x}{x}dx = \displaystyle\frac{\pi}{2}$となり、(\ref{eq:dirchletintegral})式が成り立つことがわかります。$\qquad\blacksquare$