はじめに
本Webサイトのポンチ絵的な図はInkscape 0.92.3(またはそれ以降のバージョン、2023年9月現在では1.3)で書いています。
ただ、本Webサイトを構築するにあたって本格的にInkscapeを使い始めたので、必要な機能がどこにあるかわからず、メニューバーから探し回ることが割と頻繁にあります。
そんな中、「関数のプロット」というちょっと便利そうなメニューを見つけたので、この記事で紹介しようと思います。
基本的なプロットの方法
というわけで、具体的な例を使って紹介したほうがよいと思うので、本Webサイトでは毎度おなじみの標準正規分布関数
y &= \frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}
\end{align}
を関数のプロット機能を使って描いてみます。
基本的なプロットの方法は以下の通りです。
- Inkscapeを起動します。
- 矩形ツール(下図の赤矢印)を使って長方形を描きます。
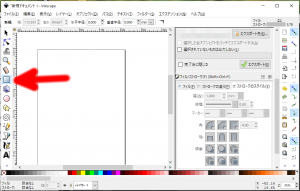
このときに、フィルに色を設定すると$x$軸とグラフの間の部分が指定された色で描画されます。また、プロットされる関数自体はストロークで指定した色で描画されます。 - メニューバーから「エクステンション」→「レンダリング」→「関数のプロット」を選択します(下図の赤矢印)。
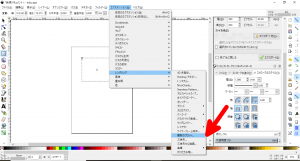
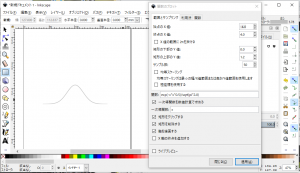
- 「関数のプロット」ウィンドウ(下図の赤矢印)が現れますので、描画時の設定を行います。
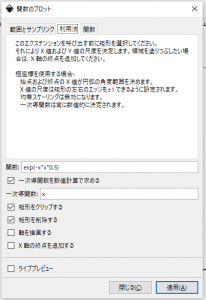
- 「関数」に下図の矢印(a)のようにプロットさせたい関数を記述します。また、「一次導関数を数値計算で求める」(下図の矢印(b))のチェックボックスにチェックを入れます。
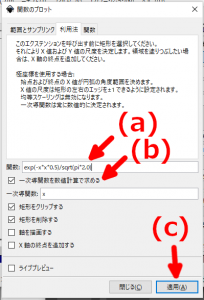
- 「関数のプロット」ウィンドウ下部の「適用」ボタン(上図の矢印(c))をクリックします。
- 下図のようなグラフが描画できます(「範囲とサンプリング」タブの設定で$x$の範囲を$-4 \le x \le 4$に調整しています)。
もうちょい触ってみた。
範囲とサンプリングの選択。
「関数のプロット」ウィンドウには「範囲とサンプリング」、「利用法」及び「関数」の3個のタブがあり、メニューで「関数のプロット」を選択した直後に表示されるウィンドウでは「利用法」のタブが選択された状態になっています。
「範囲とサンプリング」タブを選択すると$x$軸(横軸)方向や$y$軸(縦軸)方向の表示範囲(「矩形の下部のY値」及び「矩形の上部のY値」(下図の赤矢印))を設定できます。
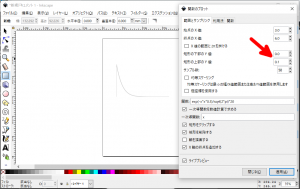
設定はできるのですが、0.1おきにしか設定ができないようで、
y &= \frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}, 3 \le x \le 6 \label{eq:threesigma}
\end{align}
のような関数(切断標準正規分布関数)をプロットしても、ただの$x$軸にしか見えない感じになってしまいます。上図では(\ref{eq:threesigma})式の右辺に20をかけた関数をプロットしています。
また、「極座標を使用する」にチェックが入っているとおそらく大多数のユーザが意図するであろう表示にはならないので、意図して極座標を使用する場合を除き、チェックを外しておきます。
多項式の入力
多項式で次数が高いものをプロットする場合に
x*x*x*…
と入力するのは面倒ですし、ミスの原因にもなりかねません。
そんなときには、「**」のようにアスタリスクを2個並べて、「x**4」($x^4$の場合)のように書くと次数の高い多項式を簡単に書くことができます。
スポンサーリンク
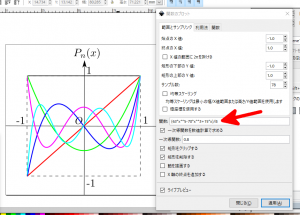
これで、「Legendre多項式の$P_5(x)$をプロットしたものをPNGファイルで頂戴❤️」などと偉い人から頼まれた場合でも、以下の赤矢印のように入力すると$P_5(x) = \displaystyle\frac{1}{8}(63x^5-70^3+15x)$がプロットできます。
まとめ
「関数のプロットができる」というのはラスタ形式では真似のできないところで、ベクタ形式の強みであると思います。
ただ、描画できる関数が$y = f(x)$や$r = g(\theta)$(極座標表示の場合)の形式のものに限られるようですので、ちょっと正確なポンチ絵やデザインの骨格のようなものを描きたいときには使えるかもしれません。
また、inkscapeには回転体を作る機能はないようですので、そんなときにはBlenderを使うと良いみたいです。
もうちょっと早く気が付けばよかった機能ですね。(´・ω・`)
この記事で書いた図をもとにして別の記事を書くわけですが、それはまた後日公開することになると思います。
panda先生の次回作にご期待ください!! (`・ω・´)
この記事は以上です。
 Inkscape(0.92.4)で積分経路を書いてから始める複素積分。
Inkscape(0.92.4)で積分経路を書いてから始める複素積分。  【動画作りました。】Windows 10にインストールしたInkscapeで描いた図の中にLaTeXの数式を直接挿入する。
【動画作りました。】Windows 10にインストールしたInkscapeで描いた図の中にLaTeXの数式を直接挿入する。  【作例を追加しました。】Inkscapeで文字の影を描画する時に、文字の描画範囲からはみ出た影がクリッピングされるのを防ぐ方法のメモ書き。
【作例を追加しました。】Inkscapeで文字の影を描画する時に、文字の描画範囲からはみ出た影がクリッピングされるのを防ぐ方法のメモ書き。 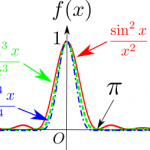 sinc関数の2,3,4乗の[0,∞)の広義積分を部分積分を使って計算する。
sinc関数の2,3,4乗の[0,∞)の広義積分を部分積分を使って計算する。