sinc関数の2,3,4乗の[0,∞)の広義積分を部分積分を使って計算する。

By | 2019年5月3日 , Last update: 2022年8月7日
0 Comment

はじめに

ちょっと前の記事でディリクレ積分の計算を行いました。

それを使ってsinc関数の積分を複素積分を使わないで計算できないかと思い、部分積分を使って計算してみたところ、4乗あたりまでなら何とか計算できそうなので、メモすることにしました。

なお、この記事では「sinc関数」は(\ref{eq:sincdef})式で表される関数$f(x)$のことを指すものとします。

\begin{align}
f(x) &= \frac{\sin x}{x} \label{eq:sincdef}
\end{align}

スポンサーリンク

順番に計算していきます。

$[0,\infty )$の広義積分を計算しますが、sinc関数の2,3,4乗はいずれも偶関数となりますので、積分区間を$(-\infty , \infty)$としたときの計算結果は積分区間を$[0,\infty )$としたときの2倍になります。

また、この記事では

\begin{align}
\int_{0}^{\infty} \frac{\sin x}{x} dx &= \frac{\pi}{2} \label{eq:dirchletintegral}
\end{align}

が成り立つことは既知とします。

sinc関数の2乗($+\alpha$)

$\displaystyle\int_{0}^{\infty} \displaystyle\frac{\sin^2 x}{x^2}dx$は部分積分を用いて以下のように変形及び計算できます。

\begin{align}
\int_{0}^{\infty} \frac{\sin^2 x}{x^2}dx &= \int_{0}^{\infty}\left(-\frac{1}{x}\right)^{\prime} \sin^2 x dx \nonumber \cr
&= \left[ -\frac{\sin^2 x}{x} \right]_{0}^{\infty} + \int_{0}^{\infty}\frac{2\cos x\sin x}{x} dx \nonumber \cr
&= \int_{0}^{\infty}\frac{\sin 2x}{x} dx \nonumber \cr
&= \displaystyle\int_{0}^{\infty}\frac{\sin t}{\displaystyle\frac{t}{2}}\cdot\displaystyle\frac{1}{2} dt \nonumber \cr &= \frac{\pi}{2} \label{eq:sincsquare}
\end{align}

なお、(\ref{eq:sincsquare})式の結果を利用すると、$a > 0$のとき、
\begin{align}
\int_{0}^{\infty} \frac{\sin^2 ax}{x^2}dx &= \int_{0}^{\infty} \frac{\sin^2 t}{\displaystyle\frac{t^2}{a^2}}\cdot\frac{dt}{a} \nonumber \cr
&= a \int_{0}^{\infty} \frac{\sin^2 t}{t}dt \nonumber \cr
&= \frac{a\pi}{2} \label{eq:sincsquareatimes}
\end{align}

であることもわかります。

sinc関数の3乗

2乗の場合と同様に、$\displaystyle\int_{0}^{\infty} \displaystyle\frac{\sin^3 x}{x^3}dx$は部分積分を用いて以下のように変形及び計算できます。

\begin{align}
\int_{0}^{\infty} \frac{\sin^3 x}{x^3}dx &= \int_{0}^{\infty}\left(-\frac{1}{2x^2}\right)^{\prime} \sin^3 x dx \nonumber \cr
&= \left[ -\frac{\sin^3 x}{2x^2} \right]_{0}^{\infty} + \int_{0}^{\infty}\frac{3\cos x\sin^2 x}{2x^2} dx \nonumber \cr
&= \int_{0}^{\infty}\frac{3\sin 2x\sin x}{4x^2} dx \nonumber \cr
&= \int_{0}^{\infty}\left(-\frac{1}{x}\right)^{\prime}\frac{3\sin 2x\sin x}{4} dx \nonumber \cr
&= \left[ -\frac{3\sin 2x\sin x}{4} \right]_{0}^{\infty} + \int_{0}^{\infty}\frac{3}{4x}(2\cos 2x\sin x + \sin 2x\cos x) dx \nonumber \cr
&= \int_{0}^{\infty}\frac{3}{4x}(\cos 2x\sin x + \sin 3x) dx \nonumber \cr
&= \int_{0}^{\infty}\frac{3}{4x}\left[\frac{1}{2}(\sin 3x-\sin x) + \sin 3x\right] dx \nonumber \cr
&= \int_{0}^{\infty}\frac{3}{4x}\left(\frac{3}{2}\sin 3x-\frac{1}{2}\sin x\right) dx \nonumber \cr
&= \frac{9}{16}\pi – \frac{3}{16}\pi \nonumber \cr
&= \frac{3}{8}\pi \label{eq:sinccube}
\end{align}

sinc関数の4乗

[2020/06/12補足] 途中の式変形に誤りがあったので、修正しました。
2乗及び3乗の場合と同様に、$\displaystyle\int_{0}^{\infty} \displaystyle\frac{\sin^4 x}{x^4}dx$は部分積分を用いて(\ref{eq:sincfourthpowerfirst})式のようにひとまず変形します。

\begin{align}
\int_{0}^{\infty} \frac{\sin^4 x}{x^4}dx &= \int_{0}^{\infty}\left(-\frac{1}{3x^3}\right)^{\prime} \sin^4 x dx \nonumber \cr
&= \left[ -\frac{\sin^4 x}{3x^3} \right]_{0}^{\infty} + \int_{0}^{\infty}\frac{4\cos x\sin^3 x}{3x^3} dx \nonumber \cr
&= \int_{0}^{\infty}\frac{2\sin 2x\sin^2 x}{3x^3} dx \nonumber \cr
&= \int_{0}^{\infty}\left(-\frac{1}{3x^2}\right)^{\prime}\sin 2x\sin^2 x dx \nonumber \cr
&= \left[ -\frac{1}{3x^2}\sin 2x\sin^2 x \right]_{0}^{\infty} + \int_{0}^{\infty}\frac{1}{3x^2}(2\cos 2x\sin^2 x + 2\sin 2x\cos x\sin x) dx \nonumber \cr
&= \int_{0}^{\infty}\frac{1}{3x^2}\left[\sin^2 2x + \cos 2x(1- \cos 2x)\right] dx
\label{eq:sincfourthpowerfirst}
\end{align}

ここで、(\ref{eq:sincfourthpowerfirst})式の右辺から$\cos 2x$を消去できないか考えます。

$\cos^2 2x = 1 – \sin^2 2x$であることを利用すると…

\begin{align}
\int_{0}^{\infty} \frac{\sin^4 x}{x^4}dx &= \int_{0}^{\infty}\frac{1}{3x^2}(2\sin^2 2x + \cos 2x – 1) dx \label{eq:sincfourthpowersecond}
\end{align}

と変形できて、さらに$\cos 2x – 1 = -2\sin^2 x$であることを利用すると…
\begin{align}
\int_{0}^{\infty} \frac{\sin^4 x}{x^4}dx &= \int_{0}^{\infty}\frac{1}{3x^2}(2\sin^2 2x – 2\sin^2 x) dx \nonumber \cr
&= \frac{2}{3}\pi – \frac{\pi}{3} \nonumber \cr
&= \frac{\pi}{3} \label{eq:sincfourthpower}
\end{align}

と計算できます。なお、最後の変形で(\ref{eq:sincsquareatimes})式を利用しています。

おまけ: sinc^2, sinc^3, sinc^4のグラフ

sinc関数の5乗の計算はできませんでした。orz

そこで、区間$\left[-2\pi,2\pi\right]$における$f(x) = \displaystyle\frac{\sin^n x}{x^n}, (n = 2,3,4)$のグラフをInkscapeで書いてみました。

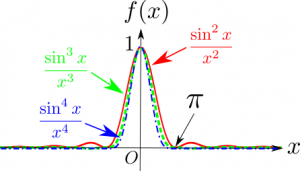
上記グラフ中、赤色の実線が$f(x) = \displaystyle\frac{\sin^2 x}{x^2}$、青色の点線が$f(x) = \displaystyle\frac{\sin^3 x}{x^3}$、緑色の一点鎖線が$f(x) = \displaystyle\frac{\sin^4 x}{x^4}$のグラフです。

まとめ

この記事で書いた2,3,4乗の計算及び途中経過については正しくない部分があるかもしれませんので、別途計算などを行った際の結果の確認用などに利用していただけると幸いです。🙇‍♂️

この記事は以上です。

References / 参考文献

Related Posts / 関連ページ

Inkscape(0.92.4)で積分経路を書いてから始める複素積分。 Inkscape 0.92.3で関数をプロットしてみた。 【作例を追加しました。】Inkscapeで文字の影を描画する時に、文字の描画範囲からはみ出た影がクリッピングされるのを防ぐ方法のメモ書き。 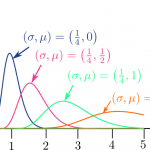対数正規分布の確率密度関数を導出して、ついでに期待値及び分散を計算してみた。