はじめに
実験データをはじめとする実世界を対象としたデータ群を統計的に扱うときにかなり高い確率で登場し、かつ何とかする必要に迫られるのが、「外れ値」です。
例えば、得られたデータが $\{ a_n \} = \{ 600,500,16000,1000,400,700,550,800,1200,900 \}$のようなものであったりすると、16000は他のデータ値と比較すると桁違いに大きいので何となく除外したくなります。
しかし、上記のデータが、
「東京の港区在住の方をランダムに10人ピックアップしたときの、各人の年収(単位:万円)。」
のようなデータだと、年収16000万円(=1.6億円)の方が(自分の周囲にはいなかったとしても)実際にはいらっしゃる可能性があるだけに、「16000」というデータは外れ値として除外してはいけないものなのかも、と思いたくなります。
こういうときにはデータを対数にすると、もしかすると正規分布みたいな分布になったりするのかもしれません(※個人のこじつけです)。
そこで、あるデータ列 $\{ a_k\} (1 \le k \le n)$ の各データに対して $b_k = \log a_k$ を考え、データ列 $\{ b_k\}$ が正規分布になるような分布を考えることにします。
対数正規分布
確率変数の変数変換の確認
前節の分布にもすでにれっきとした日本語の名称がつけられています。
「対数正規分布」といいます。
前節ではデータ列については離散的に扱いましたが、ここからは計算の都合上、連続的な確率分布について扱うことにします。
対数正規分布の確率密度関数をとりあえず$q(y) (y$を確率変数とします。$)$とおきます。
少々見慣れない形ですが、しばらくの間辛抱願います。
$q(y)$は以下の(\ref{eq:nddensity})式で表される正規分布の確率密度関数$p(x)$
スポンサーリンク
p(x) &= \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} \label{eq:nddensity}
\end{align}
からの確率変数の変換を行うことで導出することができますが、確率密度関数の導出を行う前に確率変数の変換の方法について確認しておきます。
(\ref{eq:nddensity})式の確率密度関数に従う確率変数$X$があったときに、$x \le X \le x+dx (dx > 0)$となる確率は近似的に$|p(x)dx|$と考えることができます。同様に確率密度関数$q(y)$に従う確率変数$Y$があったときに$y \le Y \le y+dy (dy > 0)$となる確率も同様に$|q(y)dy|$と考えることができます。
ここで$p(x)$及び$q(y)$が連続関数であるとすると、$dx$及び$dy$については(\ref{eq:pxqy})式が成り立つようにとることができます。
|q(y)dy| &= |p(x)dx| \label{eq:pxqy}
\end{align}
さらに(\ref{eq:pxqy})式の両辺を形式的に$|dy|$で割ります。
すると…
|q(y)| &= \left|p(x)\frac{dx}{dy}\right| \label{eq:dxqy}
\end{align}
であることがわかります。
対数正規分布の確率密度関数の導出
一方で、確率変数$Y$の対数である$X$が正規分布に従う確率変数であるため、$x$及び$y$の関係は(\ref{eq:xlogy})式の関係式で表すことができます。
x &= \log y \label{eq:xlogy}
\end{align}
そこで、(\ref{eq:xlogy})式の両辺を$y$で微分したものを(\ref{eq:dxqy})式に代入しつつ(\ref{eq:nddensity})式を用いると、(\ref{eq:logndfirst})式のように変形できます。
|q(y)| &= \left|p(\log y)\frac{d}{dy}(\log y)\right| \nonumber \cr
&= \left|p(\log y)\frac{1}{y}\right| \nonumber \cr
&= \left|\frac{1}{y}\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(\log y-\mu)^2}{2\sigma^2}}\right| \nonumber \cr
&= \left|\frac{1}{\sqrt{2\pi\sigma^2}y}e^{-\frac{(\log y-\mu)^2}{2\sigma^2}}\right| \label{eq:logndfirst}
\end{align}
$q(y)$は確率密度関数であるため$q(y) \gt 0$となります。また、(\ref{eq:logndfirst})式の右辺も$\left( -\infty, \infty \right)$で負でない値をとるため、両辺ともに絶対値記号を外すことができて…
q(y) &= \frac{1}{\sqrt{2\pi\sigma^2}y}e^{-\frac{(\log y-\mu)^2}{2\sigma^2}} \label{eq:logndsecond}
\end{align}
となります。ここまでは$q(y)$が連続関数であると仮定して計算しましたが、(\ref{eq:logndsecond})式より求まった$q(y)$は連続関数であることがわかります。
なお、(\ref{eq:logndsecond})式の変数$y$及び関数を示す記号$q$という文字自体は特別な意味を持ちません。したがって、それぞれ$x$及び$p$と書き換えても良いので…
p(x) &= \frac{1}{\sqrt{2\pi\sigma^2}x}e^{-\frac{(\log x-\mu)^2}{2\sigma^2}} \nonumber \cr
&= \frac{1}{x\sqrt{2\pi\sigma^2}}\exp\left[-\frac{(\log x-\mu)^2}{2\sigma^2}\right] \label{eq:logndfinal}
\end{align}
と書くことができます。$\blacksquare$
なお、(\ref{eq:logndfinal})式の$p(x)$の定義域は$(0,\infty)$となります。
Wikipediaの対数正規分布のページ[1]には$\mu=0$で固定して$\sigma$を変化させたときの確率密度関数のグラフが掲載されています(※この記事を最初に書いた時点(2022年3月)の情報です。)ので、$\sigma=\displaystyle\frac{1}{4}$で固定して$\mu$を変化させたときのグラフをInkscape(1.1.2)で作ってみました↓
(対数でない一般的な)正規分布の場合には$\mu$を変化させるとグラフの形は変化せずに$x$軸方向に$\mu$だけ移動しますが、対数正規分布の場合には山の頂が移動するだけでなく、グラフの形も変化することがわかります。
対数正規分布の期待値
次に、(\ref{eq:logndfinal})式に従う確率変数$X$の期待値$E[X]$について考えます。
例によって、サクサクと計算していきます。
E[X] &= \int_{0}^{\infty} xp(x)dx \nonumber \cr
&= \int_{0}^{\infty} x \frac{1}{x\sqrt{2\pi\sigma^2}}\exp\left[-\frac{(\log x-\mu)^2}{2\sigma^2}\right]dx \nonumber \cr
&= \int_{0}^{\infty} \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left[-\frac{(\log x-\mu)^2}{2\sigma^2}\right]dx \label{eq:expectionfirst}
\end{align}
とここまでは分子にあった$x$が消えてくれていい感じに計算できますが、$u = \log x$と置くとすこし様子が変わってきます。
$x$が$0 \to \infty$と変化すると$u$は$-\infty \to \infty$と変化することに注意しつつ計算を進め、(\ref{eq:expectationsecond})式のように変形します。
E[X] &= \int_{-\infty}^{\infty} \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left[-\frac{(u-\mu)^2}{2\sigma^2}\right]\frac{dx}{du}du \nonumber \cr
&= \int_{-\infty}^{\infty} \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left[-\frac{(u-\mu)^2}{2\sigma^2}\right]\frac{d(e^u)}{du}du \nonumber \cr
&= \int_{-\infty}^{\infty} \frac{e^u}{\sqrt{2\pi\sigma^2}}\exp\left[-\frac{(u-\mu)^2}{2\sigma^2}\right]du \cr
&= \int_{-\infty}^{\infty} \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left[u-\frac{(u-\mu)^2}{2\sigma^2}\right]du \label{eq:expectationsecond}
\end{align}
(\ref{eq:expectationsecond})式の$\exp[\cdot]$の$\cdot$の部分は、以下のように変形できます($u$と$\mu$は文字の形が似ていますが、めげずに計算します)。
u-\frac{(u-\mu)^2}{2\sigma^2} &= -\frac{(u-\mu)^2-2u\sigma^2}{2\sigma^2} \nonumber \cr
&= -\frac{u^2-2u\mu+\mu^2-2u\sigma^2}{2\sigma^2} \nonumber \cr
&= -\frac{u^2-2u(\mu+\sigma^2)+\mu^2}{2\sigma^2} \nonumber \cr
&= -\frac{[u-(\mu+\sigma^2)]^2-(\mu+\sigma^2)^2+\mu^2}{2\sigma^2} \nonumber \cr
&= -\frac{[u-(\mu+\sigma^2)]^2-\mu^2-2\mu\sigma^2-\sigma^4+\mu^2}{2\sigma^2} \nonumber \cr
&= -\frac{[u-(\mu+\sigma^2)]^2-2\mu\sigma^2-\sigma^4}{2\sigma^2} \nonumber \cr
&= -\frac{[u-(\mu+\sigma^2)]^2}{2\sigma^2}+\frac{2\mu\sigma^2+\sigma^4}{2\sigma^2} \nonumber \cr
&= -\frac{[u-(\mu+\sigma^2)]^2}{2\sigma^2}+\frac{2\mu+\sigma^2}{2} \label{eq:expectationthird}
\end{align}
(\ref{eq:expectationthird})式を(\ref{eq:expectationsecond})式に代入すると$\mu$及び$\sigma$は定数ですので…
E[X] &= \int_{-\infty}^{\infty} \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left[-\frac{[u-(\mu+\sigma^2)]^2}{2\sigma^2}+\frac{2\mu+\sigma^2}{2}\right]du \nonumber \cr
&= \exp\left(\frac{2\mu+\sigma^2}{2}\right) \int_{-\infty}^{\infty} \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left[-\frac{[u-(\mu+\sigma^2)]^2}{2\sigma^2}\right]du \label{eq:expectationfourth}
\end{align}
になります。ここで(\ref{eq:expectationfourth})式の右辺の被積分関数に着目すると、平均$(\mu+\sigma^2)$で分散$\sigma^2$の正規分布を表していて、かつそれを$(-\infty, \infty)$の範囲で積分することになりますが、この計算結果は1になります。
よって、
E[X] &= \exp\left(\frac{2\mu+\sigma^2}{2}\right) \label{eq:expectationfinal}
\end{align}
となることがわかります。$\blacksquare$
なお、(\ref{eq:expectationfinal})式の$\mu$及び$\sigma$は対数正規分布の平均値及び標準偏差を表すものではないことに注意が必要です。
対数正規分布の分散
次に、(\ref{eq:logndfinal})式に従う確率変数$X$の分散$V[X]$について考えます。
なお、$V[X] = E[X^2]-(E[X])^2$と表すことができて、$E[X]$については前節で計算済みですので、$E[X^2]$を計算することに注力します。
$E[X^2]$は(\ref{eq:somfirst})式のように表すことができます。
E[X^2] &= \int_{0}^{\infty} x^2p(x)dx \nonumber \cr
&= \int_{0}^{\infty} x^2 \frac{1}{x\sqrt{2\pi\sigma^2}}\exp\left[-\frac{(\log x-\mu)^2}{2\sigma^2}\right]dx \nonumber \cr
&= \int_{0}^{\infty} \frac{x}{\sqrt{2\pi\sigma^2}}\exp\left[-\frac{(\log x-\mu)^2}{2\sigma^2}\right]dx \label{eq:somfirst}
\end{align}
前節の議論と同様に、$u = \log x$とおいて、$x$が$0 \to \infty$と変化すると$u$は$-\infty \to \infty$と変化することに注意しつつ計算を進めます。
E[X^2] &= \int_{-\infty}^{\infty} \frac{e^u}{\sqrt{2\pi\sigma^2}}\exp\left[-\frac{(u-\mu)^2}{2\sigma^2}\right]\frac{dx}{du}du \nonumber \cr
&= \int_{-\infty}^{\infty} \frac{e^u}{\sqrt{2\pi\sigma^2}}\exp\left[-\frac{(u-\mu)^2}{2\sigma^2}\right]\frac{d(e^u)}{du}du \nonumber \cr
&= \int_{-\infty}^{\infty} \frac{e^{2u}}{\sqrt{2\pi\sigma^2}}\exp\left[-\frac{(u-\mu)^2}{2\sigma^2}\right]du \cr
&= \int_{-\infty}^{\infty} \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left[2u-\frac{(u-\mu)^2}{2\sigma^2}\right]du \label{eq:somsecond}
\end{align}
(\ref{eq:somsecond})式の$\exp[\cdot]$の$\cdot$の部分は、以下のように変形できます(期待値を計算した際の計算と似たような感じの計算が続きます。)。
2u-\frac{(u-\mu)^2}{2\sigma^2} &= -\frac{(u-\mu)^2-4u\sigma^2}{2\sigma^2} \nonumber \cr
&= -\frac{u^2-2u\mu+\mu^2-4u\sigma^2}{2\sigma^2} \nonumber \cr
&= -\frac{u^2-2u(\mu+2\sigma^2)+\mu^2}{2\sigma^2} \nonumber \cr
&= -\frac{[u-(\mu+2\sigma^2)]^2-(\mu+2\sigma^2)^2+\mu^2}{2\sigma^2} \nonumber \cr
&= -\frac{[u-(\mu+2\sigma^2)]^2-\mu^2-4\mu\sigma^2-4\sigma^4+\mu^2}{2\sigma^2} \nonumber \cr
&= -\frac{[u-(\mu+2\sigma^2)]^2-4\mu\sigma^2-4\sigma^4}{2\sigma^2} \nonumber \cr
&= -\frac{[u-(\mu+2\sigma^2)]^2}{2\sigma^2}+\frac{4\mu\sigma^2+4\sigma^4}{2\sigma^2} \nonumber \cr
&= -\frac{[u-(\mu+2\sigma^2)]^2}{2\sigma^2}+2\mu+2\sigma^2 \label{eq:somthird}
\end{align}
(\ref{eq:somthird})式を(\ref{eq:somsecond})式に代入すると$\mu$及び$\sigma$は定数ですので…
E[X^2] &= \int_{-\infty}^{\infty} \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left[-\frac{[u-(\mu+2\sigma^2)]^2}{2\sigma^2}+2\mu+2\sigma^2\right]du \nonumber \cr
&= \exp\left(2\mu+2\sigma^2\right) \int_{-\infty}^{\infty} \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left[-\frac{[u-(\mu+2\sigma^2)]^2}{2\sigma^2}\right]du \label{eq:somfourth}
\end{align}
になります。ここで(\ref{eq:somfourth})式の右辺の被積分関数に着目すると、平均$(\mu+2\sigma^2)$で分散$\sigma^2$の正規分布を表していて、かつそれを$(-\infty, \infty)$の範囲で積分することになりますが、この計算結果は1になります。
よって、
E[X^2] &= \exp\left(2\mu+2\sigma^2\right) \label{eq:somfinal}
\end{align}
となることがわかります。
(\ref{eq:expectationfinal})式及び(\ref{eq:somfinal})式の結果より、$V[X]$は
V[X] &= E[X^2]-(E[X])^2 \nonumber \cr
&= \exp\left(2\mu+2\sigma^2\right) – \left[\exp\left(\frac{2\mu+\sigma^2}{2}\right)\right]^2 \nonumber \cr
&= \exp\left(2\mu+2\sigma^2\right) – \exp\left(2\mu+\sigma^2\right) \nonumber \cr
&= \exp\left(2\mu+\sigma^2\right)\left[\exp(\sigma^2)-1\right] \label{eq:variancefinal}
\end{align}
と計算できます。$\blacksquare$
まとめ
(\ref{eq:logndfinal})式は変換元の正規分布の式((\ref{eq:nddensity})式)の$x$を単純に$\log x$で置き換えただけでなく、全体を$x$で割ったものになることに注意が必要です。
本記事の最初に挙げた個人の年収の分布のように外れ値にも何らかの意味があると考えられる時には正規分布に無理に当てはめるよりは対数正規分布等の他の分布関数を当てはめた方が良い場合がありそうです。
確率変数の変数変換は計算がややこしかったり間違えやすい計算になることが多いので、ついでに復習することにしました。何かのご参考にしていただけると幸いです。
この記事は以上です。
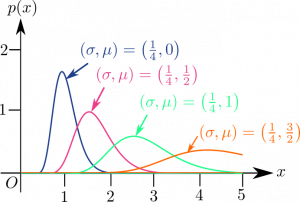
 Inkscape 0.92.3で関数をプロットしてみた。
Inkscape 0.92.3で関数をプロットしてみた。  Inkscape(0.92.4)で積分経路を書いてから始める複素積分。
Inkscape(0.92.4)で積分経路を書いてから始める複素積分。  sinc関数の2,3,4乗の[0,∞)の広義積分を部分積分を使って計算する。
sinc関数の2,3,4乗の[0,∞)の広義積分を部分積分を使って計算する。  円錐を回転体だと考えることにして、体積を計算する。
円錐を回転体だと考えることにして、体積を計算する。