はじめに
2023年2月にそれまで無料で利用できていたTwitterのAPIが有料化されるというニュースが報じられました。
本WebサイトでもWordPressのSNAP|AutoPosterプラグインを使用して、記事を新規に追加した際にお知らせをTwitterに自動的に投稿することにしていましたが、その手が使えなくなるかもしれないということで、心の準備とSNAP|AutoPosterプラグインの動作確認テスト用の記事の準備をしていました。
しかし、Twitter APIの有料化自体の開始日が2度にわたって延期された上に、使い方によっては無料のままで使えるかもしれないという情報が流れたりしていて、最終的にどのような形に落ち着くのかよくわからなくなってきました。
そこで、Twitter APIの有料化の件はひとまず考えないことにして、テスト用に用意していた記事を書いてしまうことにしました。
円錐
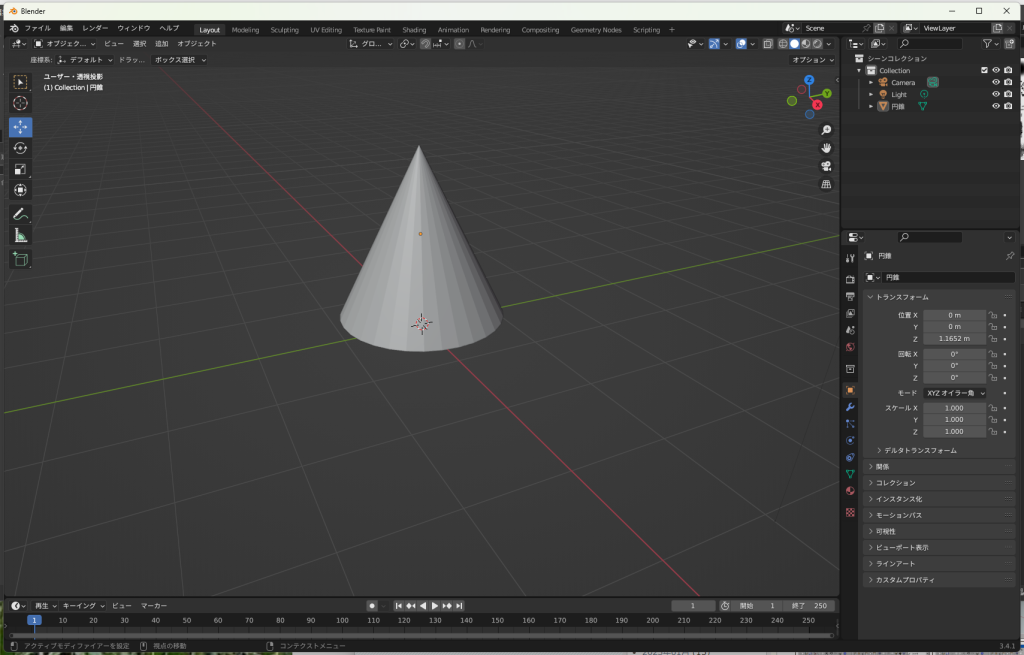
突然ですが、底面の半径が$r$で高さが$h$の円錐を考えます。
こんな形のものです↓
本Webサイトでは久々のBlender登場です。
この円錐の体積を求めます。
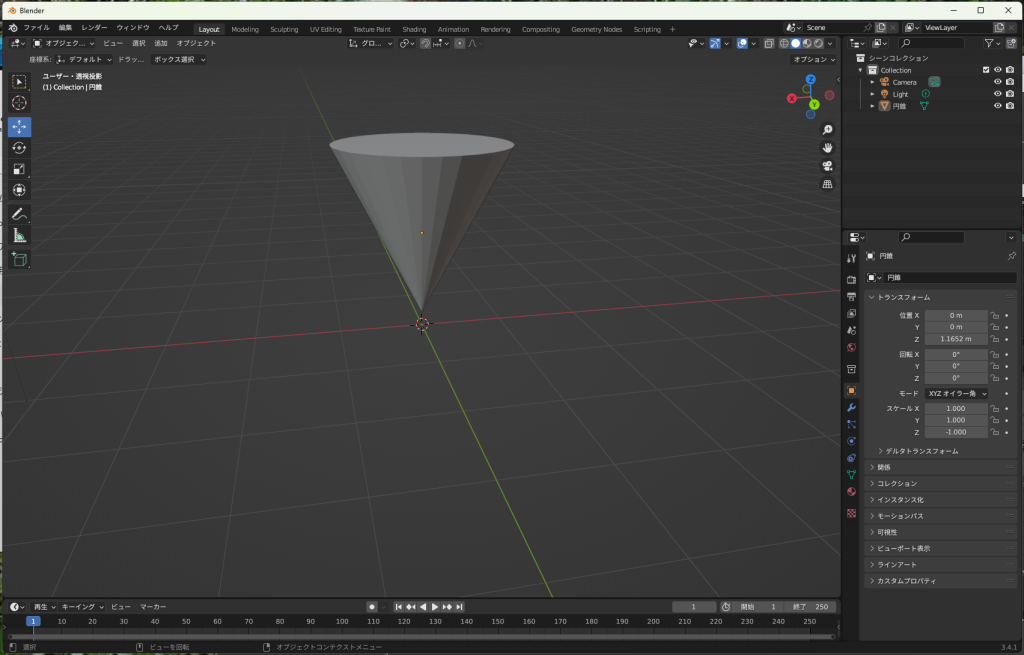
この後の計算と説明の都合上、以下のように上下を逆さにした状態の円錐があると考えます。
回転体
円錐を頂点と底面の円の中心を含んだ面で切ると、その断面は二等辺三角形になります。
二等辺三角形は等しい二辺に挟まれた角の二等分線で合同な2つの直角三角形に切ることができます。
スポンサーリンク
この直角三角形は元の円錐の頂点と底面の円の中心を頂点としていて、かつ底面の円の中心に対応する頂点は直角になります。
そこで、元の円錐の頂点と原点とし、原点から底面の円の中心に対応する頂点への向きを$y$軸の正の向きとする$xy$平面を考えると、上記の直角三角形は以下の緑色のグラデーションで塗った部分及びその境界で表すことができます。
上図の直角三角形を利用すると、元の円錐は上図の直角三角形を$y$軸の周りに一回転させたときに直角三角形が通過した部分と考えることができます。
また、直角三角形の斜辺を含む直線の方程式は、
y &= \frac{h}{r}\,x\label{eq:slopeeq}
\end{align}
と表すことができます。
切断面
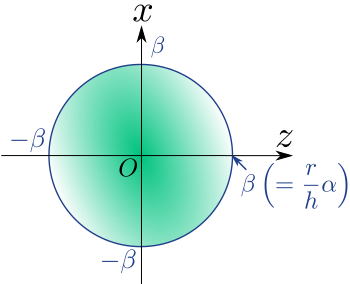
ここで、円錐を直線$y = \alpha$で切ってみます。
すると、断面は下図のような半径$\beta$の円になります。
円の内部にグラデーションがかかっていますが、特に意味はありません。
この円の面積を$\alpha$を使って表すことを考えます。
(\ref{eq:slopeeq})式を利用すると、$\alpha$と$\beta$の間には(\ref{eq:alphabeta})の関係があることがわかります。
\alpha &= \frac{h}{r}\,\beta\label{eq:alphabeta}
\end{align}
そこで、(\ref{eq:alphabeta})式を$\beta$について解くと、
\beta &= \frac{r}{h}\,\alpha\label{eq:betaalpha}
\end{align}
と書けますので、上図の円の面積$S$は半径が$\beta$であることから、
S &= \pi\left(\frac{r}{h}\,\alpha\right)^2 \nonumber \cr
&= \frac{r^2\pi}{h^2}\alpha^2 \label{eq:S}
\end{align}
となります。
$S$は$\alpha$の関数なので、ここからは$S(\alpha)$と書くことにします。
また、上図の円が実は微小な厚み$\Delta\alpha$を持つと考えると、その円柱の体積は $S(\alpha)\Delta\alpha$となります。
積分
$\alpha$は0から$h$まで変化しますので、$\alpha$は0から$h$まで変化させたときの$S(\alpha)\Delta\alpha$の総和を計算します。
すると、円錐の体積は…
\int_0^h S(\alpha)\,d\alpha &= \int_0^h\frac{r^2\pi}{h^2}\alpha^2\,d\alpha \nonumber \cr
&= \frac{r^2\pi}{h^2}\left[\frac{\alpha^3}{3}\right]_0^h \nonumber \cr
&= \frac{r^2\pi}{h^2}\frac{h^3}{3} \nonumber \cr
&= \frac{r^2h\pi}{3} \nonumber \cr
&= \frac{1}{3}\pi hr^2 \label{eq:V}
\end{align}
と計算できます。$\blacksquare$
(\ref{eq:V})式がかの有名な円錐の体積の公式です。
まとめ
2月と言えば受験シーズンということで、円錐の体積を求める公式を忘れてしまった場合や積分による面積や体積計算の方法を忘れてしまった場合、さらには円錐の体積の公式は覚えていたものの、「なんで$\dfrac{1}{3}$倍するんだっけ?」という点が気になって仕方がなくなってしまった場合などにこの記事のことを思い出していただけると幸いです。
この記事は以上です。
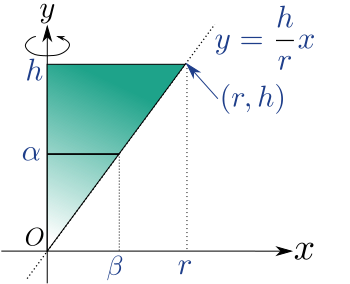
Inkscape 0.92.3で関数をプロットしてみた。 
Inkscape(0.92.4)で積分経路を書いてから始める複素積分。 
sinc関数の2,3,4乗の[0,∞)の広義積分を部分積分を使って計算する。 
対数正規分布の確率密度関数を導出して、ついでに期待値及び分散を計算してみた。 