はじめに
前の記事で、sinc関数の2,3,4乗の積分を部分計算で計算し、さらに5乗以上については部分積分では計算ができなさそうだというところまでを書きました。
部分積分を用いた帰納的なアプローチでは$\displaystyle\left(\frac{\sin x}{x}\right)^n (n \in \mathbb{N})$の計算が難しそうだな… と思いながら参考文献をもう一度よく読み直してみると、部分積分を使って分母の次数を下げてから複素積分をしているような気がするので、とりあえず数式に書き起こしてみることにしました。
以下、この記事では
I_n &= \int_{-\infty}^{\infty} \frac{\sin^n x}{x^n}dx\label{eq:sincpowerint}
\end{align}
とおいて計算していきます。
また、$\displaystyle\begin{pmatrix}
n \cr
k
\end{pmatrix}$は二項係数(${}_nC_k$)を表すこととします。二項係数の係数間には(\ref{eq:binomial})式の関係がありますが、この記事では(\ref{eq:binomial})式の関係を繰り返し使います。
\begin{pmatrix}
n \cr
k
\end{pmatrix} &= \begin{pmatrix}
n \cr
n – k
\end{pmatrix} \label{eq:binomial}
\end{align}
まず、下準備をします。
最初に$\displaystyle\frac{\sin^n x}{x^n}$を(\ref{eq:sincpower})式のように変形及び展開します。
\frac{\sin^n x}{x^n} &= \frac{(e^{ix}-e^{-ix})^n}{(2ix)^n} \nonumber \cr
&= \frac{1}{(2ix)^n}\sum_{k=0}^n (-1)^{n-k} \begin{pmatrix}
n \cr
k
\end{pmatrix} e^{ixk}e^{-ix(n-k)} \nonumber \cr
&= \frac{1}{(2i)^n}\sum_{k=0}^n (-1)^{n-k} \begin{pmatrix}
n \cr
k
\end{pmatrix} \frac{e^{ix(2k-n)}}{x^n} \label{eq:sincpower}
\end{align}
部分積分をします。
お試しに1回だけ部分積分。
(\ref{eq:sincpower})式を(\ref{eq:sincpowerint})式に代入し、部分積分による変形を1回だけ行います。
すると…
I_n &= \frac{1}{(2i)^n} \int_{-\infty}^{\infty} \sum_{k=0}^n (-1)^{n-k} \begin{pmatrix}
n \cr
k
\end{pmatrix} \left(-\frac{1}{(n-1)x^{n-1}}\right)^{\prime}e^{ix(2k-n)} dx \nonumber \cr
&= \frac{1}{(2i)^n}\left[\left[ \sum_{k=0}^n (-1)^{n-k} \begin{pmatrix}
n \cr
k
\end{pmatrix}\left[-\frac{e^{ix(2k-n)}}{(n-1)x^{n-1}}\right] \right]_{-\infty}^{\infty}\right. \nonumber \cr
&+ \left.\int_{-\infty}^{\infty} \sum_{k=0}^n (-1)^{n-k} \begin{pmatrix}
n \cr
k
\end{pmatrix} \left[\frac{i(2k-n)e^{ix(2k-n)}}{(n-1)x^{n-1}}\right]\right]dx
\label{eq:sincpowerintegralpart}
\end{align}
となります。
ところで、(\ref{eq:sincpowerintegralpart})式の第1項($J_n$とおきます。)は$n$が奇数の場合には総和をとる部分を$k
=0 \cdots \displaystyle\frac{n-1}{2}$までの前半部とそれ以降の後半部に分割し、さらに後半部については$k=n-l$とおいて変形してから、$l$を再度$k$に書き換えると、(\ref{eq:sincboundarytermatoddorder})式のように変形できます。
J_n &= \sum_{k=0}^{\frac{n-1}{2}} (-1)^{n-k} \begin{pmatrix}
n \cr
k
\end{pmatrix}\left[-\frac{e^{ix(2k-n)}}{(n-1)x^{n-1}}\right] + \sum_{k=\frac{n+1}{2}}^n (-1)^{n-k} \begin{pmatrix}
n \cr
k
\end{pmatrix}\left[-\frac{e^{ix(2k-n)}}{(n-1)x^{n-1}}\right] \nonumber \cr
&= \sum_{k=0}^{\frac{n-1}{2}} (-1)^{n-k} \begin{pmatrix}
n \cr
k
\end{pmatrix}\left[-\frac{e^{ix(2k-n)}}{(n-1)x^{n-1}}\right] + \sum_{l=0}^{\frac{n-1}{2}} (-1)^{l} \begin{pmatrix}
n \cr
n-l
\end{pmatrix}\left[-\frac{e^{ix(n-2l)}}{(n-1)x^{n-1}}\right] \nonumber \cr
&= \sum_{k=0}^{\frac{n-1}{2}} (-1)^{n-k} \begin{pmatrix}
n \cr
k
\end{pmatrix}\left[-\frac{e^{ix(2k-n)}}{(n-1)x^{n-1}}\right] + \sum_{k=0}^{\frac{n-1}{2}} (-1)^{k} \begin{pmatrix}
n \cr
n-k
\end{pmatrix}\left[-\frac{e^{ix(n-2k)}}{(n-1)x^{n-1}}\right] \nonumber \cr
&= \sum_{k=0}^{\frac{n-1}{2}} (-1)^{n-k} \begin{pmatrix}
n \cr
k
\end{pmatrix}\left[-\frac{e^{ix(2k-n)}}{(n-1)x^{n-1}}\right] + \sum_{k=0}^{\frac{n-1}{2}} (-1)^{k} \begin{pmatrix}
n \cr
k
\end{pmatrix}\left[-\frac{e^{ix(n-2k)}}{(n-1)x^{n-1}}\right] \nonumber \cr
&= \sum_{k=0}^{\frac{n-1}{2}} \begin{pmatrix}
n \cr
k
\end{pmatrix}\left[-\frac{(-1)^{n-k}e^{ix(2k-n)}+(-1)^ke^{ix(n-2k)}}{(n-1)x^{n-1}}\right] \nonumber \cr
&= \sum_{k=0}^{\frac{n-1}{2}} \begin{pmatrix}
n \cr
k
\end{pmatrix}\left[-\frac{(-1)^k\left[(-1)^{n-2k}e^{ix(2k-n)}+e^{ix(n-2k)}\right]}{(n-1)x^{n-1}}\right] \nonumber \cr
&= \sum_{k=0}^{\frac{n-1}{2}} \begin{pmatrix}
n \cr
k
\end{pmatrix}\left[\frac{(-1)^{k+1}\left[-e^{ix(2k-n)}+e^{ix(n-2k)}\right]}{(n-1)x^{n-1}}\right] \nonumber \cr
&= \sum_{k=0}^{\frac{n-1}{2}} \begin{pmatrix}
n \cr
k
\end{pmatrix}\left[\frac{2i(-1)^{k+1}\sin(n-2k)x}{(n-1)x^{n-1}}\right] \label{eq:sincboundarytermatoddorder}
\end{align}
(\ref{eq:sincboundarytermatoddorder})式右辺の総和をとる部分の各項は$x \to \infty$または$x \to -\infty$のときに0に近づきますので、$J_n \to 0$となります。
また$n$が偶数の時も総和をとる部分を$k = 0 \cdots \displaystyle\frac{n}{2}-1$までの前半部と「中央の項$\left(k = \displaystyle\frac{n}{2}\right)$」及びそれ以降の後半部に分割し、さらに後半部については$k=n-l$とおいて変形してから、$l$を再度$k$に書き換えると、奇数の場合と同様に(\ref{eq:sincboundarytermatevenorder})式のように変形できます。
J_n &= \sum_{k=0}^{\frac{n}{2}-1} (-1)^{n-k} \begin{pmatrix}
n \cr
k
\end{pmatrix}\left[-\frac{e^{ix(2k-n)}}{(n-1)x^{n-1}}\right] + \sum_{k=\frac{n}{2}+1}^n (-1)^{n-k} \begin{pmatrix}
n \cr
k
\end{pmatrix}\left[-\frac{e^{ix(2k-n)}}{(n-1)x^{n-1}}\right] + (-1)^{\frac{n}{2}} \begin{pmatrix}
n \cr
n/2
\end{pmatrix}\left[-\frac{1}{(n-1)x^{n-1}}\right] \nonumber \cr
&= \sum_{k=0}^{\frac{n}{2}-1} (-1)^{n-k} \begin{pmatrix}
n \cr
k
\end{pmatrix}\left[-\frac{e^{ix(2k-n)}}{(n-1)x^{n-1}}\right] + \sum_{k=0}^{\frac{n}{2}-1} (-1)^{k} \begin{pmatrix}
n \cr
k
\end{pmatrix}\left[-\frac{e^{ix(n-2k)}}{(n-1)x^{n-1}}\right] + (-1)^{\frac{n}{2}} \begin{pmatrix}
n \cr
n/2
\end{pmatrix}\left[-\frac{1}{(n-1)x^{n-1}}\right] \nonumber \cr
&= \sum_{k=0}^{\frac{n-1}{2}} \begin{pmatrix}
n \cr
k
\end{pmatrix}\left[-\frac{(-1)^{n-k}e^{ix(2k-n)}+(-1)^ke^{ix(n-2k)}}{(n-1)x^{n-1}}\right] + (-1)^{\frac{n}{2}} \begin{pmatrix}
n \cr
n/2
\end{pmatrix}\left[-\frac{1}{(n-1)x^{n-1}}\right] \nonumber \cr
&= \sum_{k=0}^{\frac{n-1}{2}} \begin{pmatrix}
n \cr
k
\end{pmatrix}\left[-\frac{(-1)^k\left[(-1)^{n-2k}e^{ix(2k-n)}+e^{ix(n-2k)}\right]}{(n-1)x^{n-1}}\right] + (-1)^{\frac{n}{2}} \begin{pmatrix}
n \cr
n/2
\end{pmatrix}\left[-\frac{1}{(n-1)x^{n-1}}\right] \nonumber \cr
&= \sum_{k=0}^{\frac{n-1}{2}} \begin{pmatrix}
n \cr
k
\end{pmatrix}\left[\frac{(-1)^{k+1}\left[e^{ix(2k-n)}+e^{ix(n-2k)}\right]}{(n-1)x^{n-1}}\right] + (-1)^{\frac{n}{2}} \begin{pmatrix}
n \cr
n/2
\end{pmatrix}\left[-\frac{1}{(n-1)x^{n-1}}\right] \nonumber \cr
&= \sum_{k=0}^{\frac{n-1}{2}} \begin{pmatrix}
n \cr
k
\end{pmatrix}\left[\frac{2(-1)^{k+1}\cos(n-2k)x}{(n-1)x^{n-1}}\right] + (-1)^{\frac{n}{2}} \begin{pmatrix}
n \cr
n/2
\end{pmatrix}\left[-\frac{1}{(n-1)x^{n-1}}\right]\label{eq:sincboundarytermatevenorder}
\end{align}
(\ref{eq:sincboundarytermatevenorder})式右辺第1項の総和をとる部分の各項及び右辺第2項は$x \to \infty$または$x \to -\infty$のときに0に近づきますので、$J_n \to 0$となります。
少々長くなりましたが、ここまでの議論で(\ref{eq:sincpowerintegralpart})式の第1項は0となることがわかりましたので、
I_n &= \frac{1}{(2i)^n}\int_{-\infty}^{\infty} \sum_{k=0}^n (-1)^{n-k} \begin{pmatrix}
n \cr
k
\end{pmatrix} \frac{i(2k-n)e^{ix(2k-n)}}{(n-1)x^{n-1}}dx
\label{eq:sincpowerintegralpartresult}
\end{align}
となって、部分積分を行うことにより、
- 境界積分$J_n$の値が0になること。
- 分母の$x$の次数を1つ小さくできること。
がわかります。
繰り返し部分積分します。
前節の手順を分母の$x$の次数が1になるまで繰り返すと、(\ref{eq:sincpowerintegralforcomplex})式を導くことができます。
I_n &= \frac{1}{(2i)^n}\int_{-\infty}^{\infty} \sum_{k=0}^n (-1)^{n-k} \begin{pmatrix}
n \cr
k
\end{pmatrix} \frac{[i(2k-n)]^{n-1}e^{ix(2k-n)}}{(n-1)!x}dx \label{eq:sincpowerintegralforcomplex}
\end{align}
また、(\ref{eq:sincpowerintegralforcomplex})式右辺の被積分関数は有限和ですので、$x$についての積分計算を先に行うことができます。そこで、
I_n &= \frac{1}{(2i)^n} \sum_{k=0}^n (-1)^{n-k} \begin{pmatrix}
n \cr
k
\end{pmatrix} \frac{[i(2k-n)]^{n-1}}{(n-1)!}\int_{-\infty}^{\infty}\frac{e^{ix(2k-n)}}{x}dx \label{eq:sincpowerintegralfirst}
\end{align}
と変形できます。
次に、複素積分します。
ここで、いったん$2k-n=m$とおいて、複素積分
f(z) &= \int_{-\infty}^{\infty} \frac{e^{izm}}{z} dz \label{eq:eizmdef}
\end{align}
を計算することにします。
スポンサーリンク
積分経路は$m$の値に応じて変えますので、ここからは$m$の符号に応じて場合分けとなります。なお、この記事では例によってジョルダンの補題については証明無しで利用します。
$m \gt 0$の場合
積分経路として以下の経路を考えます。
上記の積分経路が囲む領域内には$f(z)$についての特異点は存在しないことから、(\ref{eq:noresidue})式が成り立ちます。
\left( \int_{C_1} + \int_{C_2} + \int_{C_3} + \int_{C_4} \right) f(z)dz &= 0 \label{eq:noresidue}
\end{align}
ここで、経路$C_1$及び$C_3$は実軸上の経路、$C_2$は半径$R$の半円上の経路、$C_4$は半径$r$の半円上の経路を表すものとします。
$C_1$及び$C_3$は実軸上の経路なので、積分変数$z$は$x (\in {\mathbb R})$に置き換えることができて、
\left( \int_{C_1} + \int_{C_3} \right) f(z)dz &= \int_{r}^{R} \frac{e^{imx}}{x} dx + \int_{-R}^{-r} \frac{e^{imx}}{x}dx \label{eq:onrealaxis}
\end{align}
になります。
また、$C_2$は$g(z)=\displaystyle\frac{1}{z}$と置くと、$f(z) = e^{imz}g(x)$という形で書けて$m \gt 0$であり、かつ$|z| \to \infty$のときに$g(z)$が複素平面上で一様に収束するので、ジョルダンの補題を使うことができて、
\int_{C_2} f(z)dz &\to 0 \,\,(R \to \infty) \label{eq:withjordanlemma}
\end{align}
となります。
最後に、経路$C_4$に沿った積分について考えます。
$f(z)$を$z=0$のまわりでテイラー展開すると、
\frac{e^{imz}}{z} &= \frac{1}{z}\sum_{n=0}^{\infty}\frac{(imz)^n}{n!}\nonumber\cr
&= \frac{1}{z}+\sum_{n=1}^{\infty}\frac{(im)^nz^{n-1}}{n!}\nonumber\cr
&= \frac{1}{z}+\sum_{n=0}^{\infty}\frac{(im)^{n+1}z^n}{n!}\label{eq:cfourtaylor}
\end{align}
となります。
ここで$z=re^{i\theta}$と置きます。$dz=ire^{i\theta}d\theta$となることと、積分変数$\theta$についての$\pi$から$0$までの積分となることに留意しつつ(\ref{eq:cfourtaylor})式の右辺第1項を計算します。
すると…
\int_{C_4} \frac{1}{z} dz &= \int_{\pi}^{0} \frac{1}{re^{i\theta}}ire^{i\theta}d\theta \nonumber \cr
&= \int_{\pi}^{0}id\theta \nonumber \cr
&= \left[ i\theta \right]_{\pi}^{0} \nonumber \cr
&= -i\pi \label{eq:cfourfirstterm}
\end{align}
と計算でき、$r$に依存しない値となることがわかります。また、(\ref{eq:cfourtaylor})式の右辺第2項は、和と積分の順序を入れ替えることができるので、
\int_{C_4} \sum_{n=0}^{\infty}\frac{(im)^{n+1}z^n}{n!} dz &= \int_{\pi}^{0} \sum_{n=0}^{\infty}\frac{(im)^{n+1}r^ne^{in\theta}}{n!}ire^{i\theta}d\theta \nonumber \cr
&= \int_{\pi}^{0} \sum_{n=0}^{\infty}\frac{(im)^nr^{n+1}e^{i(n+1)\theta}}{n!}d\theta \nonumber \cr
&= \sum_{n=0}^{\infty} \frac{(im)^nr^{n+1}}{n!}\int_{\pi}^{0}e^{i(n+1)\theta}d\theta \label{eq:cfoursecondterm}
\end{align}
と変形できて、和の各項に$r$のべき乗が現れるので、$r \to 0$とすると、各項がすべて$0$となります。
(\ref{eq:onrealaxis}),(\ref{eq:withjordanlemma}),(\ref{eq:cfourfirstterm})及び(\ref{eq:cfoursecondterm})式を(\ref{eq:noresidue})式に代入し、$R \to \infty, r \to 0$とすると、
\int_{-\infty}^{\infty} \frac{e^{imx}}{x}dx \,- \,i\pi &= 0 \label{eq:putvalues}
\end{align}
となるので、(\ref{eq:putvalues})式の左辺第2項を右辺に移項すると、(\ref{eq:emxatpositive})式が求まります。
\int_{\infty}^{\infty} \displaystyle\frac{e^{imx}}{x}dx &= i\pi \label{eq:emxatpositive}
\end{align}
$m \lt 0$の場合
以下のような積分路を考えます。
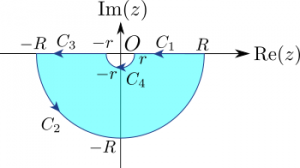
上記の積分路を設定すると$m \lt 0$の場合でも経路$C_2$においてジョルダンの補題が適用できて、(\ref{eq:withjordanlemma})式が成り立ちます。また、$C_1$及び$C_3$は実軸上の経路になりますが、向きが負の向きになりますので、
\left( \int_{C_1} + \int_{C_3} \right) f(z)dz &= \int_{R}^{r} \frac{e^{imx}}{x} dx + \int_{-r}^{-R} \frac{e^{imx}}{x}dx \label{eq:onrealaxisatnegative}
\end{align}
になります。さらに、経路$C_4$は原点のまわりの円を$2\pi$から$\pi$まで回りますので、
\int_{C_4} \frac{1}{z} dz &= \int_{\pi}^{0} \frac{1}{re^{i\theta}}ire^{i\theta}d\theta \nonumber \cr
&= \int_{2\pi}^{\pi}id\theta \nonumber \cr
&= \left[ i\theta \right]_{2\pi}^{\pi} \nonumber \cr
&= -i\pi \label{eq:cfouratnegative}
\end{align}
(\ref{eq:onrealaxisatnegative}),(\ref{eq:withjordanlemma})及び(\ref{eq:cfouratnegative})式を(\ref{eq:noresidue})式に代入し、$R \to \infty, r \to 0$とすると、
-\int_{-\infty}^{\infty} \frac{e^{imx}}{x}dx \,- \,i\pi &= 0 \label{eq:putvaluesatnegative}
\end{align}
となるので、(\ref{eq:putvalues})式の左辺第2項を右辺に移項すると、(\ref{eq:emxatnegative})式が求まります。
\int_{\infty}^{\infty} \displaystyle\frac{e^{imx}}{x}dx &= -i\pi \label{eq:emxatnegative}
\end{align}
$m = 0$の場合
$m = 0$の場合も$m \gt 0$の場合と同じ積分経路を考えると(\ref{eq:putvalues})式が成り立ちますので、積分値は(\ref{eq:emxatpositive})式と同じ値となります。
仕上げ。
…の前にちょっと細工。
(\ref{eq:emxatpositive})及び(\ref{eq:emxatnegative})式を(\ref{eq:sincpowerintegralfirst})式に代入すると積分の結果が求まるのですが、その前に(\ref{eq:sincpowerintegralfirst})式にちょっと細工をします。
$n$が偶数の場合には$2k-n=0$となる場合がありますが、(\ref{eq:sincpowerintegralfirst})式右辺の和をとる際に対応する項が0になりますので、その項は最初からなかったことにします。すなわち、
I_n &= \frac{1}{(2i)^n} \sum_{k=0,k \ne \frac{n}{2}}^n (-1)^{n-k} \begin{pmatrix}
n \cr
k
\end{pmatrix} \frac{[i(2k-n)]^{n-1}}{(n-1)!}\int_{-\infty}^{\infty}\frac{e^{ix(2k-n)}}{x}dx \label{eq:sincpowerintegralremovedatzero}
\end{align}
とします。
これにより$n$が偶数であるか奇数であるかに関係なく、和をとる対象となる項の数を偶数にすることができます。
積分の結果を元の式に反映させます。
ここまでの計算で、ようやく(\ref{eq:emxatpositive})及び(\ref{eq:emxatnegative})式を(\ref{eq:sincpowerintegralremovedatzero})式に代入することができるようになります。
$2k-n$の符号によって代入する式が異なることに注意しながら計算すると…
I_n &= \frac{1}{(2i)^n} \sum_{k=\left\lfloor\frac{n}{2}\right\rfloor+1}^{n} (-1)^{n-k} \begin{pmatrix}
n \cr
k
\end{pmatrix} \frac{[i(2k-n)]^{n-1}}{(n-1)!}\pi i + \frac{1}{(2i)^n} \sum_{k=0}^{\left\lfloor\frac{n}{2}\right\rfloor-1} (-1)^{n-k} \begin{pmatrix}
n \cr
k
\end{pmatrix} \frac{[i(2k-n)]^{n-1}}{(n-1)!}(-\pi i) \nonumber \cr
&= \frac{\pi}{(n-1)!2^n} \left[\sum_{k=\left\lfloor\frac{n}{2}\right\rfloor+1}^{n} (-1)^{n-k}(2k-n)^{n-1} \begin{pmatrix}
n \cr
k
\end{pmatrix} – \sum_{k=0}^{\left\lfloor\frac{n}{2}\right\rfloor-1} (-1)^{n-k}(2k-n)^{n-1} \begin{pmatrix}
n \cr
k
\end{pmatrix} \right]
\label{eq:sincpowerfirstresult}
\end{align}
(\ref{eq:sincpowerfirstresult})式の右辺第2項で$l=n-k$とおくと、$n$が偶数のときは負でない整数$r$を用いて$n = 2r$と表すことができて、$r = \left\lfloor\displaystyle\frac{n}{2}\right\rfloor$ですので、
n – \left( \left\lfloor\frac{n}{2}\right\rfloor-1 \right) &= r + 1 \nonumber \cr
&= \left\lfloor\frac{n}{2}\right\rfloor+1 \label{eq:niseven}
\end{align}
となります。
また、$n$が奇数のときは$n = 2r+1$と表すことができて、$r = \left\lfloor\displaystyle\frac{n-1}{2}\right\rfloor = \left\lfloor\displaystyle\frac{n}{2}\right\rfloor$ですので、
n – \left( \left\lfloor\frac{n}{2}\right\rfloor-1 \right) &= r + 1 \nonumber \cr
&= \left\lfloor\frac{n}{2}\right\rfloor+1 \label{eq:nisodd}
\end{align}
となりますので、(\ref{eq:niseven})式及び(\ref{eq:nisodd})式から、$l$は$\left\lfloor\displaystyle\frac{n}{2}\right\rfloor+1$から$n$までの整数値をとることがわかります。
そこで、(\ref{eq:sincpowerfirstresult})式を変形し、$l$を$k$に書き直すと…
I_n &= \frac{\pi}{(n-1)!2^n} \left[\sum_{k=\left\lfloor\frac{n}{2}\right\rfloor+1}^{n} (-1)^{n-k}(2k-n)^{n-1} \begin{pmatrix}
n \cr
k
\end{pmatrix} – \sum_{l=\left\lfloor\frac{n}{2}\right\rfloor+1}^{n} (-1)^{l}(n-2l)^{n-1} \begin{pmatrix}
n \cr
n – l
\end{pmatrix} \right] \nonumber \cr
&= \frac{\pi}{(n-1)!2^n} \left[\sum_{k=\left\lfloor\frac{n}{2}\right\rfloor+1}^{n} (-1)^{n-k}(2k-n)^{n-1} \begin{pmatrix}
n \cr
k
\end{pmatrix} – \sum_{k=\left\lfloor\frac{n}{2}\right\rfloor+1}^{n} (-1)^{k}(n-2k)^{n-1} \begin{pmatrix}
n \cr
k
\end{pmatrix} \right] \nonumber \cr
&= \frac{\pi}{(n-1)!2^n} \left[\sum_{k=\left\lfloor\frac{n}{2}\right\rfloor+1}^{n}\begin{pmatrix}
n \cr
k
\end{pmatrix} \left[ (-1)^{n-k}(2k-n)^{n-1} – (-1)^{k}(n-2k)^{n-1} \right] \right] \nonumber \cr
&= \frac{\pi}{(n-1)!2^n} \left[\sum_{k=\left\lfloor\frac{n}{2}\right\rfloor+1}^{n}\begin{pmatrix}
n \cr
k
\end{pmatrix} \left[ (-1)^{n-k}(2k-n)^{n-1} – (-1)^{k+n-1}(2k-n)^{n-1} \right] \right] \nonumber \cr
&= \frac{\pi}{(n-1)!2^n} \left[\sum_{k=\left\lfloor\frac{n}{2}\right\rfloor+1}^{n}\begin{pmatrix}
n \cr
k
\end{pmatrix} (2k-n)^{n-1} \left[ (-1)^{n-k} + (-1)^{k+n} \right] \right] \nonumber \cr
&= \frac{\pi}{(n-1)!2^n} \left[\sum_{k=\left\lfloor\frac{n}{2}\right\rfloor+1}^{n}\begin{pmatrix}
n \cr
k
\end{pmatrix} (2k-n)^{n-1} (-1)^{n-k} \left[ 1 + (-1)^{2k} \right] \right] \nonumber \cr
&= \frac{\pi}{(n-1)!2^n} \left[\sum_{k=\left\lfloor\frac{n}{2}\right\rfloor+1}^{n}\begin{pmatrix}
n \cr
k
\end{pmatrix} (2k-n)^{n-1} (-1)^{n-k} \cdot 2 \right] \nonumber \cr
&= \frac{\pi}{2^{n-1}}\sum_{k=\left\lfloor\frac{n}{2}\right\rfloor+1}^n (-1)^{n-k} \begin{pmatrix}
n \cr
k
\end{pmatrix} \frac{(2k-n)^{n-1}}{(n-1)!} \nonumber \cr
&= \frac{n\pi}{2^{n-1}}\sum_{k=\left\lfloor\frac{n}{2}\right\rfloor+1}^n (-1)^{n-k} \frac{(2k-n)^{n-1}}{(n-k)!k!} \label{eq:sincpowerfinalresult}
\end{align}
と変形できます。
長かったですね。😀
お好みで、ちょっと変形します。
(\ref{eq:sincpowerfinalresult})式の和をとる際の変数$k$の値の範囲が$\left\lfloor\displaystyle\frac{n}{2}\right\rfloor+1$から$n$までの整数なのは少々気持ちが悪いという方向けにちょっと変形します。
例によって$l=n-k$とおくと、$l$のとり得る値の範囲が$0$から$\left\lfloor\displaystyle\frac{n}{2}\right\rfloor-1$までの整数になりますので、
I_n &= \frac{n\pi}{2^{n-1}}\sum_{l=0}^{\left\lfloor\frac{n}{2}\right\rfloor-1} (-1)^{l} \frac{(n-2l)^{n-1}}{l!(n-l)!} \nonumber \cr
&= \frac{n\pi}{2^{n-1}}\sum_{l=0}^{\left\lfloor\frac{n}{2}\right\rfloor-1} (-1)^{l} \frac{(n-2l)^{n-1}}{l!(n-l)!} \nonumber \cr
&= \frac{n\pi}{2^{n-1}}\sum_{k=0}^{\left\lfloor\frac{n}{2}\right\rfloor-1} (-1)^{k} \frac{(n-2k)^{n-1}}{k!(n-k)!}\label{eq:sincpowerfinalresultfromzero}
\end{align}
と変形できます。
検算します。
(\ref{eq:sincpowerfinalresult})式及び(\ref{eq:sincpowerfinalresultfromzero})式が同じ値になることの確認も兼ねて$n=2,3,4,5$を代入して計算してみます。
$n=2$の場合
$\displaystyle\frac{n\pi}{2^{n-1}} = \pi$になることと、和の部分は(\ref{eq:sincpowerfinalresult})式及び(\ref{eq:sincpowerfinalresultfromzero})式の両方ともに$1$になりますので、$I_2 = \pi$となります。
$n=3$の場合
まず、$\displaystyle\frac{n\pi}{2^{n-1}}$は(\ref{eq:preludeatthree})式のように計算できます。
\frac{n\pi}{2^{n-1}} &= \frac{3}{4}\pi \label{eq:preludeatthree}
\end{align}
次に、(\ref{eq:sincpowerfinalresult})式に沿って計算します。和の部分は$k=2,3$について計算すると、その結果は1になりますので、$I_3 = \displaystyle\frac{3}{4}\pi$になります。
一方、(\ref{eq:sincpowerfinalresultfromzero})式に沿って計算する場合には、和の部分は$k=0,1$について計算します。するとその結果も1になりますので、$I_3 = \displaystyle\frac{3}{4}\pi$になります。
$n=4$の場合
まず、$\displaystyle\frac{n\pi}{2^{n-1}}$は(\ref{eq:preludeatfour})式のように計算できます。
\frac{n\pi}{2^{n-1}} &= \frac{\pi}{2} \label{eq:preludeatfour}
\end{align}
次に、(\ref{eq:sincpowerfinalresult})式に沿って計算します。和の部分は$k=3,4$について計算すると、その結果は$\displaystyle\frac{4}{3}$になりますので、$I_4 = \displaystyle\frac{2}{3}\pi$になります。
一方、(\ref{eq:sincpowerfinalresultfromzero})式に沿って計算する場合には、和の部分は$k=0,1$について計算します。すると、その結果も$\displaystyle\frac{4}{3}$になりますので、$I_4 = \displaystyle\frac{2}{3}\pi$になります。
$n=5$の場合
まず、$\displaystyle\frac{n\pi}{2^{n-1}}$は(\ref{eq:preludeatfive})式のように計算できます。
\frac{n\pi}{2^{n-1}} &= \frac{5}{16}\pi \label{eq:preludeatfive}
\end{align}
次に、(\ref{eq:sincpowerfinalresult})式に沿って計算します。和の部分は$k=3,4,5$について計算します。
だんだん計算がしんどくなってきます。
その結果は…
\frac{1}{12} – \frac{27}{8} + \frac{125}{24} &= \frac{23}{12} \label{eq:sumatfive}
\end{align}
になりますので、(\ref{eq:preludeatfive})式及び(\ref{eq:sumatfive})式をまとめて、
I_5 &= \frac{23}{12}\cdot\frac{5}{16}\pi \nonumber \cr
&= \frac{115}{192}\pi \label{eq:resultatfive}
\end{align}
になります。
一方、(\ref{eq:sincpowerfinalresultfromzero})式に沿って計算する場合には、和の部分は$k=0,1,2$について計算します。その結果は…
\frac{1}{12} – \frac{27}{8} + \frac{125}{24} &= \frac{23}{12} \label{eq:sumatfivefromzero}
\end{align}
になりますので、(\ref{eq:resultatfive})式と同様の結果を得ることができます。
まとめ
ここまでの計算で、任意の$n \in \mathbb{N}$についての$I_n$の値を求めることができました。
(\ref{eq:sincpowerint})式で$n$を大きくしたときの値を計算する行為自体には誰得感はどうしても付きまとってしまいますが、計算の途中で複素積分の計算時によく登場するジョルダンの補題の使い方や、複素平面上の極を完全に囲まない経路における複素積分の計算時の注意点(例: 2位以上の極を中心とする小さい半円上での積分はその極における留数を使って求めることができるとは限らないこと、など。)を思い出すことができるという点では、単なる頭の体操以上の価値はあるのではないかと思います。
この機会にぜひお試しください。😁
この記事は以上です。
References / 参考文献
ちょいと野暮用で正規分布に従う独立な確率変数の和と差の確率密度関数を計算してみたので、メモ書きしてみた。 
整数次数の第2種変形Bessel関数の級数表現を計算してみた。 
Inkscape(0.92.4)で積分経路を書いてから始める複素積分。 
1/(x^3+a^3)の不定積分を求めてみた。 