標準正規分布に従う2個の確率変数の商が従う確率密度関数を計算してみた。

はじめに

前の記事で、以下の確率密度関数について計算してみました。

和、差、積の次は商だと思います(※個人の感想です。)ので、標準正規分布に従う2個の確率変数の商が従う確率密度関数を計算してみることにしました。

問題の定義

まず、解くべき問題を以下のように定義します。

標準正規分布$N(0,1)$に従う2個の確率密度変数$X,Y$がある。このとき、$\displaystyle\frac{X}{Y} = Z$によって定義される確率変数$Z$が従う確率密度関数を求めよ。
ただし、$Z \ge 0$とする。

ということで積の計算に続きまして、$Z$が負の場合はとりあえず考えないことにします。(´・ω・｀)

サクサクと計算。

$Y$の符号による場合分け。

問題を定義したところで、サクサクと計算します。

まず、積分の領域を定めます。

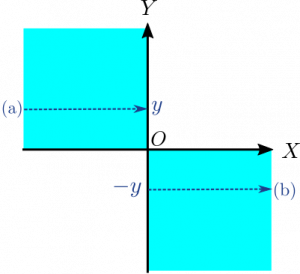
$z \ne 0$の場合、積分を実行する$X,Y$の範囲を2次元平面上にプロットすると、以下の図の水色で示した部分になります($z = 0$の場合については後述)。

$\displaystyle\frac{X}{Y} \le Z$となる$X,Y$について積分を実行していきますが、$Y$の符号によって場合分けをする必要がありそうです。また、$Y=0$の場合は$Z=\infty$になると考えることにします。(´・ω・｀)

$Z$が負の場合はとりあえず考えないことにしましたが、$Z = 0$の場合のことが気にかかるので、$X$を$Y$で割った商で定義される確率変数$Z$のとる値が$z$以下となる確率$P\left\{\displaystyle\frac{X}{Y} \le z\right\}$を$Y$の符号によって場合分けすると、(\ref{eq:Pxywithzero})式のように表すことができます。

\begin{align}
P\left\{\frac{X}{Y} \le z\right\} &= P\left\{X \le Yz,Y \ge 0\right\} + P\left\{X \ge Yz, Y \le 0\right\}\label{eq:Pxywithzero}
\end{align}

ちなみに(\ref{eq:Pxywithzero})式に$z = 0$を代入すると、

\begin{align}
P\left\{\frac{X}{Y} \le 0\right\} &= P\left\{X \le 0,Y \ge 0\right\} + P\left\{X \ge 0, Y \le 0\right\}\label{eq:Pxyatzero}
\end{align}

となります。(\ref{eq:Pxyatzero})式の積分を実行する$X,Y$の範囲を2次元平面上にプロットすると、以下の図の水色で示した部分になりますので、$Z = 0$の場合も(\ref{eq:Pxywithzero})式でまとめて考えることができそうです。

(\ref{eq:Pxywithzero})式の右辺の第1項は(\ref{eq:Pxypositive})式のように計算できます。上図の(a)の向きに最初に積分するイメージになります。なお、(\ref{eq:Pxypositive})式の右辺では$Y$を$y$と書き換えています。

\begin{align}
P\left\{X \le Yz,Y \ge 0\right\} &= \frac{1}{2\pi}\int^{\infty}_{0}e^{-\frac{y^2}{2}}dy\int^{yz}_{-\infty}e^{-\frac{x^2}{2}}dx
\label{eq:Pxypositive}
\end{align}

さらに、(\ref{eq:Pxypositive})式で$x = yu$と置きます。すると、(\ref{eq:Pxypositive})式の右辺は、

\begin{align}
P\left\{X \le Yz,Y \ge 0\right\} &= \frac{1}{2\pi}\int^{\infty}_{0}e^{-\frac{y^2}{2}}dy\int^{z}_{\infty}ye^{-\frac{(yu)^2}{2}}du
\label{eq:Pxypositivefirst}
\end{align}

と計算できます。

次に、(\ref{eq:Pxywithzero})式の右辺の第2項を計算してみます。

(\ref{eq:Pxywithzero})式の右辺の第2項は、

\begin{align}
P\left\{X \ge Yz, Y \le 0\right\} &= \frac{1}{2\pi}\int^{0}_{-\infty}e^{-\frac{y^2}{2}}dy\int^{\infty}_{yz}e^{-\frac{x^2}{2}}dx
\label{eq:Pxynegative}
\end{align}

と計算できます。上図の(b)の向きに最初に積分するイメージになります。これを(\ref{eq:Pxypositivefirst})式と似たような式に変形できないか考えてみます。

まず、$e^{-\frac{x^2}{2}}$は偶関数ですので、(\ref{eq:Pxynegative})式の右辺は(\ref{eq:Pxynegativefirst})式のように書き換えることができます。

\begin{align}
P\left\{X \ge Yz, Y \le 0\right\} &= \frac{1}{2\pi}\int^{0}_{-\infty}e^{-\frac{y^2}{2}}dy\int^{-yz}_{-\infty}e^{-\frac{x^2}{2}}dx
\label{eq:Pxynegativefirst}
\end{align}

次に、$y = -\xi$と置きます。すると、(\ref{eq:Pxynegativefirst})式の右辺は、

\begin{align}
P\left\{X \ge Yz, Y \le 0\right\} &= -\frac{1}{2\pi}\int^{0}_{\infty}e^{-\frac{\xi^2}{2}}d\xi\int^{\frac{z}{\xi}}_{-\infty}e^{-\frac{x^2}{2}}dx
\label{eq:Pxynegativesecond}
\end{align}

となりますので、さらに$x = u\xi$と置きます。すると、(\ref{eq:Pxynegativesecond})式の右辺は、

\begin{align}
P\left\{X \ge Yz, Y \le 0\right\} &= -\frac{1}{2\pi}\int^{0}_{\infty}e^{-\frac{\xi^2}{2}}d\xi\int^{z}_{-\infty}\xi e^{-\frac{(u\xi)^2}{2}}du \nonumber \\
&= \frac{1}{2\pi}\int^{\infty}_{0}e^{-\frac{\xi^2}{2}}d\xi\int^{z}_{-\infty}\xi e^{-\frac{(u\xi)^2}{2}}du
\label{eq:Pxynegativethird}
\end{align}

となります。

(\ref{eq:Pxynegativethird})式の$\xi$を$y$に置き換えると(\ref{eq:Pxypositivefirst})式の右辺と同じ式が得られます。

したがって、$P\left\{\displaystyle\frac{X}{Y} \le z\right\}$は(\ref{eq:Pxyfinal})式で表されます($u$を$x$に置き換えています)。

\begin{align}
P\left\{\frac{X}{Y} \le z\right\} &= \frac{1}{\pi}\int^{\infty}_{0}e^{-\frac{y^2}{2}}dy\int^{z}_{-\infty}ye^{-\frac{(xy)^2}{2}}dx \label{eq:Pxyfinal}
\end{align}

(\ref{eq:Pxyfinal})式の$x$及び$y$についての積分の順序は入れ替えることができます。そこで、積分の順序を入れ替えてから$z$で微分すると、$z$における確率密度関数$p(z)$が以下のように計算できます。

\begin{align}
p(z) &= \frac{1}{\pi}\int^{\infty}_{0}ye^{-\frac{y^2}{2}(1+z^2)}dy \label{eq:pzint}
\end{align}

最後の仕上げ。

和・差及び積の場合とは異なり、(\ref{eq:pzint})式が初等的な積分計算ができそうな式になりました。そこで、(\ref{eq:pzint})式で$t=y\sqrt{1+z^2}$とおきます。すると、$\displaystyle\frac{dy}{dt}=\displaystyle\frac{1}{\sqrt{1+z^2}}$となりますので(\ref{eq:pzfinal})式のように計算できます。

\begin{align}
p(z) &= \frac{1}{\pi}\int^{\infty}_{0}\frac{t}{\sqrt{1+z^2}}e^{-\frac{t^2}{2}}\frac{1}{\sqrt{1+z^2}}dt \nonumber \\
&= \frac{1}{\pi(1+z^2)}\int^{\infty}_{0}\frac{1}{t}e^{-\frac{t^2}{2}}dt \nonumber \\
&= \frac{1}{\pi(1+z^2)} \left[ -e^{-\frac{t^2}{2}} \right]^{\infty}_{0} \nonumber \\
&= \frac{1}{\pi(1+z^2)} \label{eq:pzfinal}
\end{align}

(\ref{eq:pzfinal})式は標準コーシー分布(Standard Cauchy Distribution)という確率分布です。一般的なコーシー分布は位置母数(location parameter)$z_0$及び四分位範囲$\gamma$を用いて、(\ref{eq:pzcauchy})式で表されます。

\begin{align}
p(z) &= \frac{1}{\pi\gamma} \frac{\gamma^2}{(z-z_0)^2+\gamma^2} = \frac{1}{\pi} \frac{\gamma}{(z-z_0)^2+\gamma^2}\label{eq:pzcauchy}
\end{align}

(\ref{eq:pzfinal})式は、(\ref{eq:pzcauchy})式で$\gamma = 1, z_0 = 0$と置いたものになります。

ToDoまたは検討が必要かもしれない事項

$Z \lt 0$の場合はこちらに書きましたので、ご覧いただけると幸いです。

また、$Y = 0$の場合については上図の$X$軸上での$x$について$[-\infty,\infty]$の区間における定積分を行うことになります。(\ref{eq:Pxywithzero})式右辺の第1項に$[-\infty,0]$の区間が、第2項に$[0,\infty]$の区間がそれぞれ含まれていますが、これで正しいのかどうかついては検証できていません。

まとめ

商の計算は$Y=0$のときにちょっと歯切れが悪くなってしまうのが気になるところではありますが、計算自体は積の場合と比較すると難しくはないと思います。

コーシー分布は式が簡単な割には期待値が計算できなかったりする等、かなり面白い性質を持つ関数だと思います。詳細につきましてはWikipediaの記事が詳しいので、参考にしていただけると幸いです。🙇‍♂️

この記事は以上です。

References / 参考文献

Cauchy distribution(英語版Wikipedia, 日本語版Wikipediaのページはこちら。)

おまけ

(\ref{eq:Pxywithzero})式は最初は、

\begin{align}
P\left\{\frac{X}{Y} \le z\right\} &= P\left\{\frac{X}{z} \le Y,Y \ge 0\right\} + P\left\{\frac{X}{z} \ge Y, Y \le 0\right\}\label{eq:Pxy}
\end{align}

のように書いていましたが、$z=0$ のケースが考慮できていないような気がしたので、書き換えました。