はじめに
かなり前の記事で、ちょいと野暮用で正規分布に従う2個の確率変数の和と差が従う確率密度関数を計算してみました。
この記事はその続編のようなものです。
調子に乗ってあまり使わないかもしれない標準正規分布関数に従う2個の確率変数の積を計算しようと試みたわけですが、本Webサイトの管理人たるpandaの計算の能力が未熟なせいもあってか、2018年の年末にものすごい勢いでハマってしまったので、メモっておくことにしました。✍
問題の定義
まず、解くべき問題を以下のように定義します。
標準正規分布$N(0,1)$に従う2個の確率密度変数$X,Y$がある。このとき、$XY = Z$によって定義される確率変数が従う確率密度関数を求めよ。ただし、$Z > 0$とする。
なお、なぜ$Z > 0$としたかというと、
「場合分けが面倒だからです。」
と潔く(本Webサイト比)言い切っておくことにします。
[2019/08/17 追記] $Z < 0$の場合についても別途書きました。こちらをご参照いただけると幸いです。
サクサクと計算。
$Y$の符号による場合分け。
問題を定義したところで、サクサクと計算します。
まず、積分の領域を定めます。
積分を実行する$X,Y$の範囲を2次元平面上にプロットすると、以下の図の水色で示した部分になります。
スポンサーリンク
この記事の最初の方で$Z > 0$といきなり変数の範囲を限定したにもかかわらず、$Y$の符号によって場合分けをする必要がありそうです。(´・ω・｀)
$Y$の符号を考慮しつつ、$X,Y$の積で定義される確率変数$Z$のとる値が$z$以下となる確率$P\{XY\le z\}$は(\ref{eq:Pxy})式で表されます。
[2019/01/12追記]不等号の向きが間違っていたので、修正しました。
P\{XY\le z\} &= P\{XY\le z,Y \ge 0\} + P\{XY\le z, Y \le 0\}\label{eq:Pxy}
\end{align}
(\ref{eq:Pxy})式の右辺の第1項は(\ref{eq:Pxypositive})式のように計算できます。上図の(a)の向きに最初に積分するイメージになります。なお、(\ref{eq:Pxypositive})式の右辺では$Y$を$y$と書き換えています。
P\{XY\le z,Y \ge 0\} &= \frac{1}{2\pi}\int^{\infty}_{0}e^{-\frac{y^2}{2}}dy\int^{\frac{z}{y}}_{-\infty}e^{-\frac{x^2}{2}}dx
\label{eq:Pxypositive}
\end{align}
ここで、ちょっと気になるのは$Y=0$の場合のところですが、この場合は(\ref{eq:Pxypositive})式のうち変数$x$による積分区間が$[-\infty,\infty]$になるので、
\int^{\infty}_{-\infty}e^{-\frac{x^2}{2}}dx&=\sqrt{2\pi} \label{eq:gaussian}
\end{align}
と計算できて積分可能ですので、(\ref{eq:Pxypositive})式は$Y=0$の場合にも成り立つと考えることができます。
さらに、(\ref{eq:Pxypositive})式で$x = \displaystyle{\frac{u}{y}}$と置きます。すると、(\ref{eq:Pxypositive})式の右辺は、
P\{XY\le z,Y \ge 0\} &= \frac{1}{2\pi}\int^{\infty}_{0}e^{-\frac{y^2}{2}}dy\int^{z}_{-\infty}\frac{1}{y}e^{-\frac{u^2}{2y^2}}du
\label{eq:Pxypositivefirst}
\end{align}
と計算できます。
次に、(\ref{eq:Pxy})式の右辺の第2項を計算してみます。
(\ref{eq:Pxy})式の右辺の第2項は、
P\{XY\le z,Y \le 0\} &= \frac{1}{2\pi}\int^{0}_{-\infty}e^{-\frac{y^2}{2}}dy\int^{\infty}_{\frac{z}{y}}e^{-\frac{x^2}{2}}dx
\label{eq:Pxynegative}
\end{align}
と計算できます。上図の(b)の向きに最初に積分するイメージになります。これを(\ref{eq:Pxypositivefirst})式と似たような式に変形できないか考えてみます。
まず、$e^{-\frac{x^2}{2}}$は偶関数ですので、(\ref{eq:Pxynegative})式の右辺は(\ref{eq:Pxynegativefirst})式のように書き換えることができます。
P\{XY\le z,Y \le 0\} &= \frac{1}{2\pi}\int^{0}_{-\infty}e^{-\frac{y^2}{2}}dy\int^{-\frac{z}{y}}_{-\infty}e^{-\frac{x^2}{2}}dx
\label{eq:Pxynegativefirst}
\end{align}
次に、$y = -\xi$と置きます。すると、(\ref{eq:Pxynegativefirst})式の右辺は、
P\{XY\le z,Y \le 0\} &= -\frac{1}{2\pi}\int^{0}_{\infty}e^{-\frac{\xi^2}{2}}d\xi\int^{\frac{z}{\xi}}_{-\infty}e^{-\frac{x^2}{2}}dx
\label{eq:Pxynegativesecond}
\end{align}
となりますので、さらに$x = \displaystyle{\frac{u}{\xi}}$と置きます。すると、(\ref{eq:Pxynegativesecond})式の右辺は、
P\{XY\le z,Y \le 0\} &= -\frac{1}{2\pi}\int^{0}_{\infty}e^{-\frac{\xi^2}{2}}d\xi\int^{z}_{-\infty}\frac{1}{\xi}e^{-\frac{u^2}{2\xi^2}}du \nonumber \\
&= \frac{1}{2\pi}\int^{\infty}_{0}e^{-\frac{\xi^2}{2}}d\xi\int^{z}_{-\infty}\frac{1}{\xi}e^{-\frac{u^2}{2\xi^2}}du
\label{eq:Pxynegativethird}
\end{align}
となります。
(\ref{eq:Pxynegativethird})式の$\xi$を$y$に置き換えると(\ref{eq:Pxypositivefirst})式の右辺と同じ式が得られます。
したがって、$P\{XY\le z\}$は(\ref{eq:Pxyfinal})式で表されます($u$を$x$に置き換えています)。
P\{XY\le z\} &= \frac{1}{\pi}\int^{\infty}_{0}e^{-\frac{y^2}{2}}dy\int^{z}_{-\infty}\frac{1}{y}e^{-\frac{x^2}{2y^2}}dx \label{eq:Pxyfinal}
\end{align}
(\ref{eq:Pxyfinal})式の$x$及び$y$についての積分の順序は入れ替えることができます。そこで、積分の順序を入れ替えてから$z$で微分すると、$z$における確率密度関数$p(z)$が以下のように計算できます。
p(z) &= \frac{1}{\pi}\int^{\infty}_{0}\frac{e^{-\frac{y^2}{2}-\frac{z^2}{2y^2}}}{y}dy \label{eq:pzfinal}
\end{align}
さらに変数変換。
ここからは結論がある程度見えていないと計算をするモチベーションが起こりにくいところではありますが、(\ref{eq:pzfinal})式をすでによく知られた形に変形できないか考えてみます。
(\ref{eq:pzfinal})式で$t=\displaystyle\frac{y^2}{2}$とおきます。すると、$\displaystyle\frac{dy}{dt}=\displaystyle\frac{1}{\sqrt{2t}}$となりますので(\ref{eq:pandt})式のように変形できます。
p(z) &= \frac{1}{\pi}\int^{\infty}_{0}\frac{1}{\sqrt{2t}}e^{-2t-\frac{z^2}{4t}}\frac{1}{\sqrt{2t}}dt \nonumber \\
&= \frac{1}{2\pi}\int^{\infty}_{0}\frac{1}{t}e^{-2t-\frac{z^2}{4t}}dt\label{eq:pandt}
\end{align}
最後の仕上げに、$t = \displaystyle\frac{ze^{\eta}}{2}$とおきます。(\ref{eq:pandt})式の積分区間は$[0,\infty]$ですが、$\eta$の積分区間は$[-\infty,\infty]$となることと、$\displaystyle\frac{dt}{d\eta} = \displaystyle\frac{ze^{\eta}}{2}$であることから、
p(z) &= \frac{1}{2\pi}\int^{\infty}_{-\infty}\frac{1}{\displaystyle\frac{ze^{\eta}}{2}}\exp\left[-2\frac{ze^{\eta}}{2}-\frac{z^2}{4\frac{ze^{\eta}}{2}}\right]\frac{ze^{\eta}}{2}d\eta \nonumber \\
&= \frac{1}{2\pi}\int^{\infty}_{-\infty}\exp\left[-\frac{ze^{\eta}}{2}-\frac{z}{2e^{\eta}}\right]d\eta \nonumber \\
&= \frac{1}{2\pi}\int^{\infty}_{-\infty}\exp\left[-z\frac{e^{\eta}+e^{-\eta}}{2}\right]d\eta \nonumber \\
&= \frac{1}{2\pi}\int^{\infty}_{-\infty}\exp\left[-z\cosh(\eta)\right]d\eta \label{eq:expcosh}
\end{align}
となります。
ここで、(\ref{eq:expcosh})式の右辺の$\exp(\cdot)$の$\cdot$の部分をじーっと見ると、$z$は$\eta$に依存しない定数であり、$\cosh(\eta)$は偶関数であることから、(\ref{eq:expcosh})式の右辺は、
((\ref{eq:expcosh})式の右辺) &= \frac{1}{\pi}\int^{\infty}_{0}\exp\left[-z\cosh(\eta)\right]d\eta \label{eq:expcoshfinal}
\end{align}
となります。
(\ref{eq:expcoshfinal})式は0次の第2種変形Bessel関数(Modified Bessel Function of the Second Kind, $K_0(z)$)の積分表示を$\pi$で割ったものに等しくなりますので、確率密度関数$p(z)$は(\ref{eq:pzbessel})式のように表すことができます。
p(z) &= \frac{K_0(z)}{\pi} \label{eq:pzbessel}
\end{align}
おまけ
この記事を最初に書いた時点(2019年1月)では実際に計算してみたわけではありませんが、$z < 0$の場合は前節の同様の手順で(\ref{eq:pzbesselminus})式となることを示すことができます。
[2019/01/12追記] こちらのページに書きました。
p(z) &= \frac{K_0(-z)}{\pi} \label{eq:pzbesselminus}
\end{align}
そこで、(\ref{eq:pzbessel})式及び(\ref{eq:pzbesselminus})式をまとめて(\ref{eq:pzbesselabs})式と書くこともできます。
p(z) &= \frac{K_0(|z|)}{\pi} \label{eq:pzbesselabs}
\end{align}
まとめ
2019年は新年最初の記事からいきなり最初から数式満載の記事でお送りしてみました。
[2019/01/12,2019/02/06追記]ちょこちょこと間違っているところがあったので、修正しました。
$p(z)$を0次の第2種変形Bessel関数で表すために変数の変換を何回か繰り返していますが、最後の$t = \displaystyle\frac{ze^{\eta}}{2}$とおいたところで置き換え後の積分の範囲が誤っていたことに気づかず、どうしても分母の2が取れずにハマってしまいました。
今後気を付けます。
Bessel関数は日常生活においてはそう簡単に登場することはないと思いますが、何かの参考にしていただけると幸いです。🙇♂️
この記事は以上です。
References / 参考文献
- Bessel function (英語版Wikipedia)
夏が来れば思い出す、Euler角、四元数(1): ちょっと計算してみた。 
標準正規分布の確率密度関数をテイラー展開してから積分して累積分布関数を求めてみた。 
重箱の隅過ぎて伝わらないZiggurat法: tailの部分の計算方法がなんでそうなるのか調べてみた。 
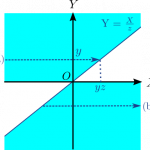標準正規分布に従う2個の確率変数の商が従う確率密度関数を計算してみた。 