標準正規分布の確率密度関数をテイラー展開してから積分して累積分布関数を求めてみた。

はじめに

前の記事で正規分布に従う2個の独立な確率変数の和と差の確率密度関数を計算しました。

Google先生に聞いてみたり、思い出しながら書いているためにところどころ用語の使い方が怪しい部分があるかもしれませんが、そのあたりは気づき次第修正します。

前の記事でちょっとエンジンがかかってきたところで、この記事では標準正規分布の確率密度関数をテイラー展開し、さらにそいつを積分して累積分布関数を計算してみます。

ついでに収束判定のところで少し寄り道をします。

テイラー展開します。

本記事では冪乗及び階乗の計算式が頻繁に登場しますが、$0^0 = 1, 0! = 1, 0!! = 1$とします。

指数関数のテイラー展開

指数関数の$x=0$のまわりにおけるテイラー展開は(\ref{eq:exptaylor})式で表されます。

\begin{align}
e^x &= \sum_{n=0}^{\infty}\frac{x^n}{n!} \label{eq:exptaylor}
\end{align}

次節以降の話の展開の都合上、$e^{-x}$を$x=0$のまわりでテイラー展開した式が必要になるので、以下((\ref{eq:exptaylorminus})式)に示しておきます。

\begin{align}
e^{-x} &= \sum_{n=0}^{\infty}(-1)^n\frac{x^n}{n!} \label{eq:exptaylorminus}
\end{align}

標準正規分布の確率密度関数のテイラー展開

次に、標準正規分布の確率密度関数の$x=0$のまわりにおけるテイラー展開を計算します。

といっても、テイラー展開の(一般的な)展開式

\begin{align}
f(x) &= \sum_{n=0}^{\infty}(-1)^n\frac{x^n}{n!}f^{(n)}(0) \label{eq:taylor}
\end{align}

に

\begin{align}
p(x) &= \frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}} \label{eq:gaussian}
\end{align}

を直接当てはめようとして、$f^{\prime}(x),f^{\prime\prime}(x),f^{(3)}(x),\cdots$を順次計算してみたところで収拾がつかなくなるだけなので、ここは前節の結果を利用することを考えます。

(\ref{eq:exptaylorminus}),(\ref{eq:taylor})及び(\ref{eq:gaussian})式をじーっと見比べると、$f(x) = e^{-x}$とおいて、さらに$f\left(\displaystyle\frac{x^2}{2}\right)$を(\ref{eq:exptaylorminus})式を使って計算してみると、

\begin{align}
f\left(\displaystyle\frac{x^2}{2}\right) &= \frac{1}{\sqrt{2\pi}}\sum_{n=0}^{\infty}\frac{(-1)^n}{n!}\left(\displaystyle\frac{x^2}{2}\right)^n \nonumber \\
&= \frac{1}{\sqrt{2\pi}}\sum_{n=0}^{\infty}\frac{(-1)^n\,x^{2n}}{(2n)!!} \label{eq:gausstaylor}
\end{align}

(ただし、$(2n)!! = \displaystyle\prod_{k=1}^n2k$とします。)となります。

収束することの確認。

標準正規分布の確率密度関数は(\ref{eq:gausstaylor})式の通りに計算ができそうですが、(\ref{eq:gausstaylor})式の右辺が収束することを示さないと使い物になりません。(\ref{eq:gausstaylor})式の左辺をあらためて$f(x)$と置きなおして、右辺を$x$の級数と考えると、級数の各項の係数$\{a_n\} (n \ge 0)$は

\begin{align}
a_n &=
\begin{cases}
\displaystyle\frac{1}{\sqrt{2\pi}}\displaystyle\frac{(-1)^k}{(2k)!!} & (n: even, n = 2k) \\
0 & (otherwise)
\end{cases} \label{eq:coefficient}
\end{align}

となります。

ここで、ダランベールの収束判定法を使いたい… ところではありますが、(\ref{eq:coefficient})式より、隣接する項のどちらか片方が0になりますので、そのままでは使用できません。

そこで、ここはコーシーの冪根判定法を使用します。(\ref{eq:coefficient})式の$a_n$より、

\begin{align}
\sqrt[n]{|a_n|} &=
\begin{cases}
\displaystyle\frac{1}{\sqrt[2n]{2\pi}}\displaystyle\frac{1}{\sqrt[n]{n!!}} > 0 & (n: even, n = 2k) \\
0 & (otherwise)
\end{cases}
\end{align}

となることと、$\displaystyle\lim_{n \to \infty} \displaystyle\frac{1}{\sqrt[n]{n!!}} = 0$であること(証明はこちら参照… と最初は書いていたのですが、参照先では$\displaystyle\lim_{n \to \infty} \displaystyle\frac{1}{\sqrt[n]{\color{red}{n!}}} = 0$を証明してました(汗)。これをもとに$\displaystyle\lim_{n \to \infty} \displaystyle\frac{1}{\sqrt[n]{n!!}} = 0$は証明できます。証明の方法はこちらに書きました。)から、$\displaystyle\limsup_{n \to \infty} a_n = 0 < 1$になります。したがって(\ref{eq:gausstaylor})式の級数は($x$について)収束することがわかります。

累積分布関数を計算します。

この節では、前節の結果を利用して累積分布関数を計算します。なお、この節では累積分布関数を$P(x)$と置きます。

積分します。

まず、不定積分を計算してみます。(\ref{eq:gausstaylor})式は$x$について項別積分できますので、積分定数をCとすると、

\begin{align}
P(x) &= \int p(x) dx \nonumber \\
&= \frac{1}{\sqrt{2\pi}}\int \left\{ \sum_{n=0}^{\infty}\frac{(-1)^n\,x^{2n}}{(2n)!!} \right\}dx \nonumber \\
&= \frac{1}{\sqrt{2\pi}}\sum_{n=0}^{\infty}\frac{(-1)^n}{(2n+1)\,(2n)!!}x^{2n+1}+C
\end{align}

となります。

次に、$P(0)=1/2$であることを利用すると$C=1/2$となります。

したがって、$P(x)$は(\ref{eq:solution})式のように定まります。

\begin{align}
P(x) &= \frac{1}{\sqrt{2\pi}}\sum_{n=0}^{\infty}\frac{(-1)^n}{(2n+1)\,(2n)!!}x^{2n+1}+\frac{1}{2} \label{eq:solution}
\end{align}

もうちょい変形。

数学的には(\ref{eq:solution})式の形で良いような気もしますが、ここまで計算できると、実際に検算してみたくなります。

そこで$a_n = \displaystyle\frac{(-1)^n}{(2n+1)\,(2n)!!}$とおいて、以下のように変形します。

すると、$a_0 = 1$なので、

\begin{align}
P(x) &= \frac{1}{\sqrt{2\pi}} \sum_{n=0}^{\infty} a_n x^{2n+1}+\frac{1}{2} \nonumber \\
&= \frac{1}{\sqrt{2\pi}} \left\{ a_0x + a_0x\sum_{n=1}^{\infty} \left( \prod_{k=0}^{n-1}\frac{a_{k+1}}{a_k}x^2 \right) \right\}+\frac{1}{2} \nonumber \\
&= \frac{x}{\sqrt{2\pi}} \left\{ 1 + \sum_{n=1}^{\infty} \left( \prod_{k=0}^{n-1}\frac{-(2k+1)}{(2k+2)(2k+3)}x^2 \right) \right\}+\frac{1}{2} \label{eq:solutionseries}
\end{align}

収束があまり速くなさそうな気もしますが、上式のように変形すると級数の前の項の係数の計算結果及び変数$x$並びに項番号$k$のみを使って次の項の係数を計算することができるようになります。

プログラムを書いて検算です。

(\ref{eq:solutionseries})式が導けたので、正しいかどうか以下のようなプログラムを書いて確認してみます。なお、テスト用のプログラムですので、デバッグ用と思しき出力が残っているのはご容赦いただければと思います。

コードを差し替えました。[2018/09/03追記,2018/09/16計算式を訂正]

normDist関数中のwhile文のループの継続条件を変化率の絶対値($a_nx^{2n+1}$を直前の項($n-1$項)までの$P(x)$の計算結果で割った値の絶対値)が$10^{-12}$以上である場合に変更しています(なお、コードの差し替え前は$|a_nx^{2n+1}| > 10^{-12}$である場合としていました)。

これに伴い、いわゆる「ゼロ割りエラー」が発生するのを防止するため、normDist関数の引数に0が指定された場合には計算を行わずに0.5を返すためのコードを関数の先頭部分に追加しました。

Excelと答え合わせ。

実はExcelの関数に同様の計算を行うもの(NORM.S.DIST関数)がありますので、その結果と照らし合わせて確認してみます。

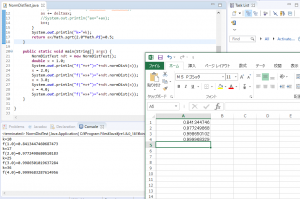
正しい計算結果を返していることが確認できました。(｀・ω・´)ｼｬｷｰﾝ

まとめ

ここまでの考察で確率密度関数が正規分布である確率変数がある値$x$以下の値をとる確率を計算するための計算式で、かつプログラムで比較的容易に実装できるものを導出し、実際にプログラムとして実装して動作を確認してみました。

前項の動作確認で$x=4.0$で小数点以下10桁程度の精度の計算が36回の反復計算($a_0$の計算を除く)でできていたので、最初の予想よりは計算の効率は良いと思います。$x$に10とか100とかといった極端な値を指定されてしまった場合には、精度との兼ね合いで反復計算を行わず、1.0(または0.0)を返してしまう実装にするのもありだとは思いますが、それはシステムなどに関数を実装して組み込むときに解決せねばならない課題ですね。

この記事は以上です。