はじめに
記事のタイトルにいきなり$\LaTeX$のコマンドのようなものを入れてしまっていてすみませんが、ちょっと前の記事で証明を省略してしまった件について書きたいと思います。
っていうか、計算用紙に書いてみると…
(※字が雑なので、モザイク処理をしています。)
また後で使いそうな気がしてきたので、メモ書きしておくことにしたわけですが、ちょっと前の記事で証明が必要だった式とは異なる式を最初は証明していたので、本来証明すべき式についての証明を問題(2)として追加しています。
問題(1)
以下の問題を解くことを考えます。
$n$を自然数とするとき、$\displaystyle\lim_{n\to\infty}\sqrt[n]{n!} = \infty$であることを証明せよ。
証明していきます。
まず、$a_n=\sqrt[n]{n!}$とおいて、両辺の自然対数を取ります。すると、
\log a_n &= \log \sqrt[n]{n!} \nonumber \\
&= \frac{1}{n} \log n! \nonumber \\
&= \frac{1}{n} \sum_{k=1}^{n}\log k \label{eq:logk}
\end{align}
と変形できます。
$k=1$のときには$\log k=0$となるので、$k \ge 2$の場合を考えます。すると、関数$\log x$は$x \gt 0$で連続かつ単調増加ですので、$k-1 \le x \le k$で
\log(k-1) &\le \log x \le \log k \label{eq:k-1tok}
\end{align}
となります。次に、(\ref{eq:k-1tok})式の各辺を$[k-1,k]$の区間で$x$について積分すると、最左辺及び最右辺は$x$については定数ですので、
\log(k-1) &\le \int_{k-1}^k \log x dx \le \log k \label{eq:intk-1tok}
\end{align}
になります。
$k=1$のときには$\log k=0$となることと、(\ref{eq:intk-1tok})式の2番目の不等号の両側の辺に着目し、2から$n$までの和をとると、
\int_{1}^{n} \log x dx &\le \sum_{k=2}^{n} \log k \nonumber \\
&= \sum_{k=1}^{n} \log k \label{eq:intklogk}
\end{align}
となります。また、(\ref{eq:intklogk})の右辺は
\int_{1}^{n} \log x dx &= \left[ x\log x – x \right]_1^n \nonumber \\
&= n\log n – n + 1 \label{eq:logxdx}
\end{align}
と計算できます。
そこで、(\ref{eq:logxdx})式の両辺に$\displaystyle\frac{1}{n}$をかけて、さらに(\ref{eq:intklogk})式及び(\ref{eq:logk})式の関係を利用すると、
\frac{1}{n}\int_{1}^{n} \log x dx &= \log n – 1 + \frac{1}{n} \nonumber \\
&\le \frac{1}{n}\sum_{k=1}^{n} \log k = \log a_n \label{eq:evaluation}
\end{align}
$\displaystyle\lim_{n\to\infty}\left(\log n – 1 + \frac{1}{n}\right) = \infty$であることと、(\ref{eq:evaluation})式の関係より、$\displaystyle\lim_{n\to\infty} \log a_n = \infty$となりますので、$\displaystyle\lim_{n\to\infty} a_n = \infty$となります。$\blacksquare$
問題(2)
以下の問題を解くことを考えます。赤文字で示した部分が問題(1)とは異なる部分です。
$n$を偶数とするとき、$\displaystyle\lim_{n\to\infty}\sqrt[n]{\color{red}{n!!}} = \infty$であることを証明せよ。
証明していきます。
$n=2m$とおき、さらに$a_m=\sqrt[2m]{2m!!}$とおくと、
a_m &= \sqrt[2m]{2m!!} \nonumber \\
&= \sqrt[2m]{2^m m!} \nonumber \\
&= \sqrt{2\sqrt[m]{m!}} \label{eq:am}
\end{align}
と変形できます。$m$は自然数であるから、問題(1)より$\displaystyle\lim_{m\to\infty}\sqrt[m]{m!} = \infty$であるので、$\displaystyle\lim_{m\to\infty} a_m = \infty$になります。よって$\displaystyle\lim_{n\to\infty}\sqrt[n]{\color{red}{n!!}} = \infty$となります。$\blacksquare$
まとめ
問題(1)及び問題(2)の式を見ると直感的には発散しそうだなと思うのですが、実際に証明するとなると、この記事に書いたような感じの計算を行うことになると思います。
実は$n$乗根が$\LaTeX$では\sqrt[n]{}のような書き方ができることにこの記事を書いていて気が付きました。(´・ω・`)
この記事は以上です。
 Inkscape(0.92.4)で積分経路を書いてから始める複素積分。
Inkscape(0.92.4)で積分経路を書いてから始める複素積分。 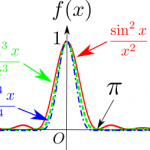 sinc関数の2,3,4乗の[0,∞)の広義積分を部分積分を使って計算する。
sinc関数の2,3,4乗の[0,∞)の広義積分を部分積分を使って計算する。  フーリエ変換再{n}入門?
フーリエ変換再{n}入門?