はじめに
ちょいと野暮な用事で正規分布に従う独立な確率変数の和と差の確率密度関数を計算しなければならなくなりそうなので、そもそもしっかり勉強していたのかどうかも思い出せませんが、思い出すことにしました。
なお、本記事では連続型の確率変数及び確率密度関数のみについて考えることにします。
まずは和の公式から。
正規分布に従う確率変数に限らず、一般に独立な確率変数$X$,$Y$とそれらに対応する確率密度関数$p_1(x),p_2(x) (x \in \mathbb{R})$について、確率変数の和$X+Y$の確率密度関数$p(x)$は以下の式で計算できます。
p(x) &=& \int^{\infty}_{-\infty}\,p_1(x-y)p_2(y)dy \label{eq:probsum}
\end{eqnarray}
(\ref{eq:probsum})式の導出は自力でやろうとしたものの、力尽きました。＿|￣|○
自分にとってわかりにくかったのは、以下のポイントだったので、後で思い出せるようにメモしておきます。
- 最終目的は確率密度関数を求めるのですが、まず、確率を計算し、それから微分すること。
- 足し合わせる2個の確率変数が独立であるかどうか確認すること。独立でない場合は別の導出方針を考える必要があります(参考文献[1])。
- 積分順序の交換が可能な条件については積分の前に必ず確認すること。
畳み込み積分の計算。
(\ref{eq:probsum})式が理解できたところで、$p(x)$を計算してみます。
$p_1(x)$が平均$\mu_1$,分散$\sigma_1^2$の正規分布の確率密度関数で、$p_2(x)$が平均$\mu_2$,分散$\sigma_2^2$の正規分布の確率密度関数とすると、$p_1(x)$及び$p_2(x)$は(\ref{eq:probden1})及び(\ref{eq:probden2})式で表すことができます。
p_1(x) &=& \frac{1}{\sqrt{2\pi}\sigma_1}e^{-\frac{(x-\mu_1)^2}{2\sigma_1^2}} \label{eq:probden1} \\
p_2(x) &=& \frac{1}{\sqrt{2\pi}\sigma_2}e^{-\frac{(x-\mu_2)^2}{2\sigma_2^2}} \label{eq:probden2}
\end{eqnarray}
(\ref{eq:probden1})及び(\ref{eq:probden2})式を(\ref{eq:probsum})式に代入して計算していきます。
すると…
p(x) &=& \frac{1}{2\pi\sigma_1\sigma_2}\int^{\infty}_{-\infty}\exp\left\{-\frac{(x-y-\mu_1)^2}{2\sigma_1^2}-\frac{(y-\mu_2)^2}{2\sigma_2^2}\right\}dy \label{eq:probden}
\end{eqnarray}
となります。次は、
\int^{\infty}_{-\infty}e^{\frac{(x-\mu)^2}{b}}dx &=& \sqrt{b\pi} \label{eq:gaussformula}
\end{eqnarray}
が適用できる形に持ち込みたいので、(\ref{eq:probden})式右辺の$\exp\left\{\cdot\right\}$を$\exp\left\{-\displaystyle\frac{1}{2}(\cdot)\right\}$と変形した上で、$(\cdot)$の部分を$y$について平方完成させます。これは、
\def\xmumu{\displaystyle\frac{x-\mu_1}{\sigma_1^2}+\displaystyle\frac{\mu_2}{\sigma_2^2}}
\def\sigmasigma{\displaystyle\frac{1}{\sigma_1^2}+\displaystyle\frac{1}{\sigma_2^2}}
&{}& \frac{(x-y-\mu_1)^2}{\sigma_1^2}+\frac{(y-\mu_2)^2}{\sigma_2^2} \nonumber \\
&=& y^2\left(\frac{1}{\sigma_1}+\frac{1}{\sigma_2}\right)-2y\left(\xmumu\right)+\frac{(x-\mu_1)^2}{\sigma_1^2}+\frac{\mu_2^2}{\sigma_2^2} \nonumber \\
&=& \left(\sigmasigma\right)\left\{y-\frac{\xmumu}{\sigmasigma}\right\}^2 + \frac{(x-\mu_1)^2}{\sigma_1^2}+\frac{\mu_2^2}{\sigma_2^2}-\frac{\left(\xmumu\right)^2}{\sigmasigma} \label{eq:sq}
\end{eqnarray}
と平方完成することができます。
本当に平方完成ができるのかちょっと先行きに不安を覚える(どのくらい不安かというと、この記事の計算くらい不安です。)ところですが、ここは少し我慢して、(\ref{eq:sq})の右辺の式のうち、平方完成から外れた部分をもう少し計算してみます。
スポンサーリンク
すると…
\def\xmumu{\displaystyle\frac{x-\mu_1}{\sigma_1^2}+\displaystyle\frac{\mu_2}{\sigma_2^2}}
\def\sigmasigma{\displaystyle\frac{1}{\sigma_1^2}+\displaystyle\frac{1}{\sigma_2^2}}
\def\sigmasigmap{\sigma_1^2+\sigma_2^2}
&{}& \frac{(x-\mu_1)^2}{\sigma_1^2}+\frac{\mu_2^2}{\sigma_2^2}-\frac{\left(\xmumu\right)^2}{\sigmasigma} \nonumber \\
&=& \frac{(x-\mu_1)^2}{\sigma_1^2}+\frac{\mu_2^2}{\sigma_2^2}-\frac{\displaystyle\frac{(x-\mu_1)^2}{\sigma_1^4} + \displaystyle\frac{2(x-\mu_1)\mu_2}{\sigma_1^2\sigma_2^2} + \displaystyle\frac{\mu^2}{\sigma_2^4}}{\sigmasigma} \nonumber \\
&=& \frac{(x-\mu_1)^2}{\sigma_1^2}+\frac{\mu_2^2}{\sigma_2^2}-\frac{1}{\sigma_1^2+\sigma_2^2}\left\{\frac{\sigma_2^2}{\sigma_1^2}(x-\mu_1)^2+2(x-\mu_1)\mu_2+\frac{\sigma_1^2}{\sigma_2^2}\mu_2^2\right\} \nonumber \\
&=& \left\{\frac{1}{\sigma_1^2}-\frac{\sigma_2^2}{\sigma_1^2(\sigmasigmap)}\right\}(x-\mu_1)^2 – \frac{1}{\sigmasigmap}\cdot 2(x-\mu_1)\mu_2+ \nonumber \\
&{}& \left\{\frac{1}{\sigma_2^2}-\frac{\sigma_1^2}{\sigma_2^2(\sigmasigmap)}\right\}\mu_2^2 \nonumber \\
&=& \frac{1}{\sigmasigmap}\left\{(x-\mu_1)^2 – 2(x-\mu_1)\mu_2 + \mu_2^2 \right\} \nonumber \\
&=& \frac{(x – \mu_1 – \mu_2)^2}{\sigmasigmap} \label{eq:residualerror}
\end{eqnarray}
(\ref{eq:sq})及び(\ref{eq:residualerror})式を利用して、(\ref{eq:probden})式の右辺を書き換えると、
\def\xmumu{\displaystyle\frac{x-\mu_1}{\sigma_1^2}+\displaystyle\frac{\mu_2}{\sigma_2^2}}
\def\sigmasigma{\displaystyle\frac{1}{\sigma_1^2}+\displaystyle\frac{1}{\sigma_2^2}}
\def\sigmasigmap{\sigma_1^2+\sigma_2^2}
p(x) &=& \frac{1}{2\pi\sigma_1\sigma_2}{\Huge\int}_{-\infty}^{\infty}\!\!\!\exp\left[-\frac{1}{2}\left\{\left(\sigmasigma\right)\left(y-\frac{\xmumu}{\sigmasigma}\right)^2\right.\right. \nonumber \\
&{}&\left.\left. +\frac{1}{\sigmasigmap}(x – \mu_1 – \mu_2)^2\right\}\right]dy \nonumber \\
&=& \frac{1}{2\pi\sigma_1\sigma_2}e^{-\frac{(x – \mu_1 – \mu_2)^2}{2(\sigmasigmap)}} \nonumber \\
&{}& {\Huge\int}_{-\infty}^{\infty}\!\!\!\exp\left[-\frac{1}{2}\left\{\left(\sigmasigma\right)\left(y-\frac{\xmumu}{\sigmasigma}\right)^2\right\}\right]dy \label{eq:probdensqres}
\end{eqnarray}
となります。
(\ref{eq:probdensqres})式右辺の被積分関数は$b = \displaystyle\frac{2}{\displaystyle\frac{1}{\sigma_1^2}+\displaystyle\frac{1}{\sigma_2^2}}, \mu = \frac{\displaystyle\frac{x-\mu_1}{\sigma_1^2}+\displaystyle\frac{\mu_2}{\sigma_2^2}}{\displaystyle\frac{1}{\sigma_1^2}+\displaystyle\frac{1}{\sigma_2^2}}$と置くと、(\ref{eq:gaussformula})式より、
\def\xmumu{\displaystyle\frac{x-\mu_1}{\sigma_1^2}+\displaystyle\frac{\mu_2}{\sigma_2^2}}
\def\sigmasigma{\displaystyle\frac{1}{\sigma_1^2}+\displaystyle\frac{1}{\sigma_2^2}}
\def\sigmasigmap{\sigma_1^2+\sigma_2^2}
{\Huge\int}_{-\infty}^{\infty}\!\!\!\exp\left[-\frac{1}{2}\left\{\left(\sigmasigma\right)\left(y-\frac{\xmumu}{\sigmasigma}\right)^2\right\}\right]dy &=& \sqrt{\frac{2\pi}{\sigmasigma}} \label{eq:insideofint}
\end{eqnarray}
と計算できます。そこで、これを(\ref{eq:probdensqres})式に代入すると、
\def\xmumu{\displaystyle\frac{x-\mu_1}{\sigma_1^2}+\displaystyle\frac{\mu_2}{\sigma_2^2}}
\def\sigmasigma{\displaystyle\frac{1}{\sigma_1^2}+\displaystyle\frac{1}{\sigma_2^2}}
\def\sigmasigmap{\sigma_1^2+\sigma_2^2}
p(x) &=& \frac{1}{2\pi\sigma_1\sigma_2}\sqrt{\frac{2\pi}{\sigmasigma}}e^{-\frac{(x – \mu_1 – \mu_2)^2}{2(\sigmasigmap)}} \nonumber \\
&=& \frac{1}{\sqrt{2\pi(\sigmasigmap)}}e^{-\frac{(x – \mu_1 – \mu_2)^2}{2(\sigmasigmap)}} \label{eq:results}
\end{eqnarray}
となります。
((\ref{eq:probden1})及び(\ref{eq:probden2})式と(\ref{eq:results})式をよく見比べると、$p(x)$は平均$\mu_1+\mu_2$,分散$\sigma_1^2+\sigma_2^2$の正規分布になっていることがわかります。よって、確率変数の和$X+Y$はこの確率密度関数$p(x)$に従うことがわかります。
差の公式の計算です。
前節の計算で確率変数の和が従う確率密度関数が計算できたので、次は確率変数の差$X-Y$が従う確率密度関数$q(x)$を計算します。
独立な確率変数$X$,$Y$とそれらに対応する確率密度関数$q_1(x),q_2(x) (x \in \mathbb{R})$について、確率変数の差$X-Y$の確率密度関数$q(x)$は以下の式で計算できます。
q(x) &=& \int^{\infty}_{-\infty}\,q_1(x+y)q_2(y)dy \label{eq:probsub}
\end{eqnarray}
和の場合と同様に、(\ref{eq:probsub})式に(\ref{eq:probden1})及び(\ref{eq:probden2})式を代入して計算していきます。$q_1(x+y)$に関連する項については符号が変わるところがありますが、(\ref{eq:insideofint})式に相当する積分については和の場合に計算した被積分関数が$x$方向に平行移動したものを$(-\infty,\infty)$で積分するので、計算結果は和の場合と等しくなります。また、(\ref{eq:residualerror})式に相当する$y$についての定数項は(細かい計算は省略しますが)、
\def\xmumup{\displaystyle\frac{\mu_2}{\sigma_2^2}-\displaystyle\frac{x-\mu_1}{\sigma_1^2}}
\def\sigmasigma{\displaystyle\frac{1}{\sigma_1^2}+\displaystyle\frac{1}{\sigma_2^2}}
\def\sigmasigmap{\sigma_1^2+\sigma_2^2}
\frac{(x-\mu_1)^2}{\sigma_1^2}+\frac{\mu_2^2}{\sigma_2^2}-\frac{\left(\xmumup\right)^2}{\sigmasigma} &=& \frac{1}{\sigmasigmap}(x-\mu_1+\mu_2)^2 \label{eq:residualerrorsub}
\end{eqnarray}
になります。よって、(\ref{eq:insideofint})及び(\ref{eq:residualerrorsub})式より
\def\xmumu{\displaystyle\frac{x-\mu_1}{\sigma_1^2}+\displaystyle\frac{\mu_2}{\sigma_2^2}}
\def\sigmasigma{\displaystyle\frac{1}{\sigma_1^2}+\displaystyle\frac{1}{\sigma_2^2}}
\def\sigmasigmap{\sigma_1^2+\sigma_2^2}
q(x) &=& \frac{1}{2\pi\sigma_1\sigma_2}\sqrt{\frac{2\pi}{\sigmasigma}}e^{-\frac{(x – \mu_1 + \mu_2)^2}{2(\sigmasigmap)}} \nonumber \\
&=& \frac{1}{\sqrt{2\pi(\sigmasigmap)}}e^{-\frac{(x – \mu_1 + \mu_2)^2}{2(\sigmasigmap)}} \label{eq:resultssub}
\end{eqnarray}
と計算できます。
(\ref{eq:probden1})及び(\ref{eq:probden2})式と(\ref{eq:resultssub})式の結果より、$q(x)$は平均$\mu_1-\mu_2$,分散$\sigma_1^2+\sigma_2^2$の正規分布になっていることがわかります。よって、確率変数の差$X-Y$はこの確率密度関数$q(x)$に従うことがわかります。
まとめのようなもの
ここまでの計算で、確率密度関数が正規分布になる独立な確率変数の和と差が従う確率密度関数について計算することができました。計算の結果得られた結論はいたってシンプルかつ基本的なものかもしれませんが、結論だけを暗記しているだけだと、いざというときに使えない気がしたので、思い出しついてに計算してみた次第です。
なお、今まで数学的な話題が含まれている記事については、「数学的チラシの裏」というカテゴリーを設定していましたが、カテゴリー名としていろいろとアレな感じもしていたので、「pandaの大計算用紙」というカテゴリー名に変更しました。この方が本サイトのタイトルとの整合性も取れて、なかなかいい感じだと思います(※個人の感想です)。
また、ついでと言っては何ですが確率密度関数が標準正規分布になる独立な確率変数の積が従う確率密度関数も計算してみました。変形Bessel関数が登場します。詳しくはこちらを参照です。
この記事は以上です。
参考文献
- [1]確率変数の和の分布を計算する【確率論、畳み込み】
- [2]独立確率変数の和の分布1
- [3]独立確率変数の和の分布2
- その他、各大学の先生方の講義資料多数。
整数次数の第2種変形Bessel関数の級数表現を計算してみた。 
ディリクレ積分をフーリエ変換を使って計算しようとしたらいろいろと出てきたので、まとめてメモ。 
Inkscape(0.92.4)で積分経路を書いてから始める複素積分。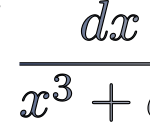 
1/(x^3+a^3)の不定積分を求めてみた。 