Legendre多項式の直交性を最高次の項の係数だけを計算することにより証明してみた。

はじめに

タイトルだけ見るとただの手抜き計算のように見えなくもないですが、次のLegendre多項式について以下の(1)式が成り立つことを(1)式の被積分関数の最高次以外の項の係数がすべて0になることを示してから、最高次の項の係数を計算することによって示します。

なお、はCroneckerのデルタを表します。

サクサクと証明します。

Legendre多項式を2通りの方法で表します。

(1)式の被積分関数に含まれる及びは入れ替えることができますので、一般性を失うことなくとすることができます。

はについての次の多項式なので、適当な係数を用いて、

と表すことができます。そこで、(2)式を(1)式の左辺に代入すると、和と積分の順序は交換できますので、

と変形できます。

一方で、は、

と表すこともできます。

部分積分を計算します。

ここで、(3)式及び(4)式から積分計算に関係する部分を抽出し、

とおいて計算します。積分計算に関係しない(4)式のについては積分計算後に再度まとめ直します。

(5)式を部分積分を用いて変形すると…

と計算できます。

次に、(6)式の右辺第1項を計算してみます。まず、

と置くと、のときに、

となります(Leibnizの公式を利用)。

ここで、であることから、 及び であるので、となります。

よって、(6)式の右辺第1項は0になりますので、

と計算できます。

ここまでの部分積分をあと回繰り返すと、部分積分を実行するごとに(6)式の右辺第1項に相当する部分が現れ、かつそれらがすべて0になりますので…

となります。

の場合には(10)式はさらに積分できます。そこで、(8)式の結果を利用すると、の場合も含めてとなりますので、

となります。

一方の場合にはとおいてから偶関数であることを利用して式を変形すると、Wallis積分が現れて、

と計算できますので、(10)式及び(12)式より、

と計算できます。

さらに、(11)式及び(13)式はまとめることができて、

と書くことができます。

部分積分の結果を利用して、計算を続行します。

スポンサーリンク

ここで本題に戻ります。

(3)式(4)式及び(14)式より、のときは、

のときは

となります。は次の多項式であることと、(16)式の結果より、(3)式の右辺で総和の計算の対象となっている各項はの場合にはすべて0となります。よって、

であることがわかります。

また、の場合も総和の計算の対象となっている各項のうち、の項はすべて0となりますので、(15)式の結果を利用して、

と計算できることがわかります。

あとはを求めると、(18)式の値が定まることになります。

ここで、が(4)式で表されるの最高次(次)の項の係数であったことを思い出すと、

ですので、これを(18)式に代入すると…

と、拍子抜けするほど簡単な式になります。

ただ、これが求めていた結果なわけで、(20)式及び(17)式から(1)式が成り立つことが証明できました。

おまけ

その1: Wallis積分

前節までの証明の途中で何の断りもなくWallis積分が登場していますが、これは及び関数の整数乗の積分について、以下の関係が成り立つというものです。ここでは負でない整数とします。

Wallis積分の概要等についてはWikipedia等をご参照ください。

また、Wikipediaの記事がわかりにくいようであれば、こちらもご参照いただけると幸いです。

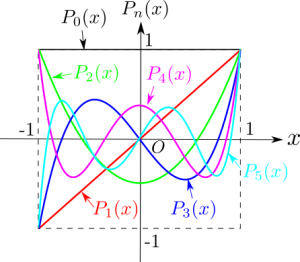
その2: Legendre多項式のグラフの描画例

Inkscapeで描いたの時ののグラフを以下に示します。

まとめ

の回未満の回数の微分を考えるところが技巧的かつあまり正攻法でないようにも見えますが、最高次の項の係数の計算に注力することができますので、比較的計算のしやすい方法であると思います(※個人の感想です)。

この記事は以上です。