はじめに
ゼータ関数のうち、$\zeta(2)$は
\zeta(2) &= \sum_{n=1}^{\infty}\frac{1}{n^2} \nonumber\cr
&= \frac{\pi^2}{6} \label{eq:basel}
\end{align}
と表すことができます。
この結果を使って$\zeta(4)$の計算ができないか考えてみることにしました。
ζ(2)を計算する
最初に$\zeta(2)$をフーリエ変換を使って求めます。
とりあえず、(\ref{eq:fonex})式の関数を考えます。
f_1(x)&= x^2 (x \in \left[ -\pi, \pi \right])\label{eq:fonex}
\end{align}
(\ref{eq:fonex})式をフーリエ展開すると、(\ref{eq:fonex})式は偶関数であることから、
f_1(x) &= \frac{a_0}{2} + \sum_{n=1}^{\infty} a_n\cos nx\label{eq:fonefourier}
\end{align}
ただし、
a_n &= \frac{1}{\pi}\int_{-\pi}^{\pi}f_1(t)\cos nt\, dt \nonumber \cr
&= \frac{1}{\pi}\int_{-\pi}^{\pi}t^2\cos nt\, dt \label{eq:fonecoefficient}
\end{align}
となりますので、(\ref{eq:fonecoefficient})式の右辺を計算します。
n > 0の場合
$n \gt 0$の場合は、(\ref{eq:fonecoefficient})式の右辺は部分積分を使って計算します。
スポンサーリンク
すると…
a_n &= \frac{1}{\pi}\int_{-\pi}^{\pi}t^2\left(\frac{1}{n}\sin nt\right)^{\prime}\, dt \nonumber\cr
&= \frac{1}{n\pi}\left(\left[t^2\sin nt\right]_{-\pi}^{\pi}-\int_{-\pi}^{\pi}2t\sin nt\, dt\right) \nonumber\cr
&= \frac{1}{n\pi}\left(-\int_{-\pi}^{\pi}2t\sin nt\, dt\right)\nonumber\cr
&= \frac{1}{n\pi}\int_{-\pi}^{\pi}2t\left(\frac{1}{n}\cos nt\right)^{\prime}\, dt\nonumber\cr
&= \frac{2}{n^2\pi}\left(\left[t\cos nt\right]_{-\pi}^{\pi}-\int_{-\pi}^{\pi}\cos nt\, dt\right)\nonumber\cr
&= \frac{2}{n^2\pi}\left((-1)^n\pi-(-1)^n(-\pi)-\left[\frac{1}{n}\sin nt\right]_{-\pi}^{\pi}\right)\label{eq:fonecoefficientsecond}\cr
&= (-1)^n\frac{4}{n^2}\label{eq:fonecoefficientthird}
\end{align}
と計算できます。なお、(\ref{eq:fonecoefficientsecond})式の計算には$n$が整数の時に$\cos nx=(-1)^n$になることを、(\ref{eq:fonecoefficientthird})式の計算には$n$が整数の時に$\sin nx=0$になることをそれぞれ利用しています。
n = 0の場合
$n = 0$の場合は(\ref{eq:fonecoefficient})式は、
a_0 &= \dfrac{1}{\pi}\int_{-\pi}^{\pi}f(t)dt \nonumber \cr
&= \dfrac{1}{\pi}\int_{-\pi}^{\pi}t^2\,dt\nonumber\cr
&= \dfrac{1}{\pi}\left[\displaystyle\frac{t^3}{3}\right]_{-\pi}^{\pi}\nonumber\cr
&= \frac{2\pi^2}{3}\label{eq:fonecoefficientatzero}
\end{align}
と計算できます。
仕上げ
(\ref{eq:fonecoefficientthird})式及び(\ref{eq:fonecoefficientatzero})式を(\ref{eq:fonefourier})式に代入すると…
f_1(x) &= \frac{\pi^2}{3} + \sum_{n=1}^{\infty}(-1)^n\frac{4}{n^2}\cos nx \label{eq:fonefourierfinal}
\end{align}
となります。
ここで、(\ref{eq:fonefourierfinal})式に$x=\pi$を代入すると、$\cos nx = (-1)^n$になりますので、
f_1(\pi) &= \frac{\pi^2}{3} + \sum_{n=1}^{\infty}(-1)^n\frac{4}{n^2}(-1)^n\nonumber\cr
&= \frac{\pi^2}{3} + \sum_{n=1}^{\infty}\frac{4}{n^2}\label{eq:squareofpi}
\end{align}
と計算できます。
(\ref{eq:squareofpi})式の右辺は$\pi^2$に等しいので…
\sum_{n=1}^{\infty}\frac{4}{n^2} &= \dfrac{2\pi^2}{3} \label{eq:baselsecond}
\end{align}
と計算できます。
よって、(\ref{eq:baselsecond})式の両辺を4で割ると、
\sum_{n=1}^{\infty}\frac{1}{n^2} &= \dfrac{\pi^2}{6} \label{eq:baselfinal}
\end{align}
となることが示せます。$\blacksquare$
ζ(4)を計算する
$\zeta(2)$の計算ができたところで、この記事の本題である$\zeta(4)$の計算に移ります。
まず、(\ref{eq:ftwox})式の関数を考えます。
f_2(x)&= x^4 (x \in \left[ -\pi, \pi \right])\label{eq:ftwox}
\end{align}
(\ref{eq:ftwox})式をフーリエ展開すると、(\ref{eq:ftwox})式は偶関数であることから、
f_2(x) &= \frac{a_0}{2} + \sum_{n=1}^{\infty} a_n\cos nx\label{eq:ftwofourier}
\end{align}
ただし、
a_n &= \frac{1}{\pi}\int_{-\pi}^{\pi}f(t)\cos nt\, dt \nonumber \cr
&= \frac{1}{\pi}\int_{-\pi}^{\pi}t^4\cos nt\, dt \label{eq:ftwocoefficient}
\end{align}
となりますので、(\ref{eq:ftwocoefficient})式の右辺を計算します。
n > 0の場合
$\zeta(2)$の場合と同様に、$n \gt 0$の場合は、(\ref{eq:ftwocoefficient})式の右辺は部分積分を使って計算します。
(\ref{eq:ftwocoefficient})式の積分の被積分関数に$t^4$が含まれているので計算量が多くなりそうですが、頑張って計算していきます。
すると…
a_n &= \frac{1}{\pi}\int_{-\pi}^{\pi}t^4\left(\frac{1}{n}\sin nt\right)^{\prime}\, dt \nonumber\cr
&= \frac{1}{n\pi}\left(\left[t^4\sin nt\right]_{-\pi}^{\pi}-\int_{-\pi}^{\pi}4t^3\sin nt\, dt\right) \nonumber\cr
&= \frac{1}{n\pi}\left(-\int_{-\pi}^{\pi}4t^3\sin nt\, dt\right)\nonumber\cr
&= \frac{1}{n\pi}\int_{-\pi}^{\pi}4t^3\left(\frac{1}{n}\cos nt\right)^{\prime}\, dt\nonumber\cr
&= \frac{1}{n^2\pi}\left(\left[4t^3\cos nt\right]_{-\pi}^{\pi}-\int_{-\pi}^{\pi}12t^2\cos nt\, dt\right)\nonumber\cr
&= \frac{1}{n^2\pi}\left(\left[4t^3\cos nt\right]_{-\pi}^{\pi}-12\int_{-\pi}^{\pi}t^2\cos nt\, dt\right)\label{eq:ftwocoefficientsecond}
\end{align}
ここで、(\ref{eq:fonecoefficient})式及び(\ref{eq:fonecoefficientthird})式より、
\int_{-\pi}^{\pi}t^2\cos nt\, dt &= (-1)^n\frac{4\pi}{n^2} \label{eq:ftwocoefficientthird}
\end{align}
であることがわかるので、(\ref{eq:ftwocoefficientthird})式を(\ref{eq:ftwocoefficientsecond})式に代入して…
\frac{1}{n^2\pi}\left(\left[4t^3\cos nt\right]_{-\pi}^{\pi}-12\int_{-\pi}^{\pi}t^2\cos nt\, dt\right) &= \frac{1}{n^2\pi}\left( 8\pi^3(-1)^n – 12 (-1)^n\frac{4\pi}{n^2}\right)\nonumber\cr
&= \frac{1}{n^2\pi}\left( 8\pi^3(-1)^n – 48 (-1)^n\frac{\pi}{n^2}\right)\nonumber\cr
&= \frac{(-1)^n}{n^2}\left( 8\pi^2 – \frac{48}{n^2}\right)\label{eq:ftwocoefficientfourth}
\end{align}
と計算できます。
n = 0の場合
$n = 0$の場合は(\ref{eq:ftwocoefficient})式は、
a_0 &= \dfrac{1}{\pi}\int_{-\pi}^{\pi}f(t)dt \nonumber \cr
&= \dfrac{1}{\pi}\int_{-\pi}^{\pi}t^4\,dt\nonumber\cr
&= \dfrac{1}{\pi}\left[\displaystyle\frac{t^5}{5}\right]_{-\pi}^{\pi}\nonumber\cr
&= \frac{2\pi^4}{5}\label{eq:ftwocoefficientatzero}
\end{align}
と計算できます。
仕上げ
(\ref{eq:ftwocoefficientfourth})式及び(\ref{eq:ftwocoefficientatzero})式を(\ref{eq:ftwofourier})式に代入すると、$f_2(x)$は
f_2(x) &= \frac{\pi^4}{5} + \sum_{n=1}^{\infty}\frac{(-1)^n}{n^2}\left( 8\pi^2 – \frac{48}{n^2}\right) \cos nx \label{eq:ftwofourierfinal}
\end{align}
とフーリエ級数展開できます。
(\ref{eq:ftwofourierfinal})式で$x = \pi$とすると、$\cos n\pi = (-1)^n$ですので…
f_2(\pi) &= \frac{\pi^4}{5} + \sum_{n=1}^{\infty}\frac{(-1)^n}{n^2}\left( 8\pi^2 – \frac{48}{n^2}\right) (-1)^n \nonumber\cr
&= \frac{\pi^4}{5} + \sum_{n=1}^{\infty}\frac{1}{n^2}\left( 8\pi^2 – \frac{48}{n^2}\right) \nonumber\cr
&= \frac{\pi^4}{5} + \sum_{n=1}^{\infty}\frac{1}{n^2}\left( 8\pi^2 – \frac{48}{n^2}\right)\nonumber\cr
&= \frac{\pi^4}{5} + \sum_{n=1}^{\infty}\frac{8\pi^2}{n^2} – \sum_{n=1}^{\infty}\frac{48}{n^4}\nonumber\cr
&= \frac{\pi^4}{5} + 8\pi^2\sum_{n=1}^{\infty}\frac{1}{n^2} – \sum_{n=1}^{\infty}\frac{48}{n^4}\label{eq:ftwoatpi}
\end{align}
と計算できます。
(\ref{eq:ftwoatpi})式の右辺第2項は(\ref{eq:baselfinal})式の結果を利用することで、
f_2(\pi) &= \frac{\pi^4}{5} + 8\pi^2\frac{\pi^2}{6} – \sum_{n=1}^{\infty}\frac{48}{n^4}\nonumber\cr
&= \pi^4\left(\frac{1}{5} + \frac{4}{3}\right) – \sum_{n=1}^{\infty}\frac{48}{n^4}\nonumber\cr
&= \frac{23}{15}\pi^4-\sum_{n=1}^{\infty}\frac{48}{n^4} \label{eq:equation}
\end{align}
となります。
(\ref{eq:equation})式の右辺は$\pi^4$に等しいことから…
\frac{8}{15}\pi^4 &= \sum_{n=1}^{\infty}\frac{48}{n^4} \label{eq:equationsecond}
\end{align}
であることがわかりますので、(\ref{eq:equationsecond})式の両辺を48で割ると…
\sum_{n=1}^{\infty}\frac{1}{n^4} &= \frac{8}{15\cdot48}\pi^4 \nonumber\cr
&= \frac{\pi^4}{90} \label{eq:zetaatfour}
\end{align}
となり、$\zeta(4) = \displaystyle\frac{\pi^4}{90}$であることがわかります。$\blacksquare$
まとめ
$s$が偶数の場合の$\zeta(s)$については漸化式があるとWikipediaに書いてあったので、$\zeta(2)$の計算結果を使うと$\zeta(4)$の計算ができるのではないかと考えたのですが、なんとか計算できました。
また、$\zeta(2)$の計算の途中で得られた式を使うことによって部分積分の計算を一部省略することができました。部分積分の計算は間違えやすい上に計算量が削減できますので、助かりますね。
この記事は以上です。
フーリエ変換再{n}入門? 
標準正規分布の確率密度関数をテイラー展開してから積分して累積分布関数を求めてみた。 
Inkscape 0.92.3で関数をプロットしてみた。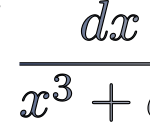 
1/(x^3+a^3)の不定積分を求めてみた。 