FREE WIFIへのアクセスを得るための積分計算。

はじめに

Twitterのタイムラインに時々流れてくることがあるFREE WIKIのパスワードを得るための積分式を計算することにしました。

問題の積分式はこちらです↓

pic.twitter.com/FB8I08vrAO

— NO CONTEXT HUMANS (@HumansNoContext) January 16, 2023

式の右側の平方根の中にが含まれているのはおそらくは何かの間違いなのだろうと思うことにして、

(1)

を計算することにします。

まず、( $1$ )式右辺の括弧を展開してみます。

すると…

(2)

となります。

( $2$ )式右辺第1項の不定積分を求めるのは難しそうなので、積分の区間に着目すると、となっていることがわかります。

積分区間がの形になっていますので、第1項の被積分関数が偶関数や奇関数だったりしないかどうか調べます。

第1項の被積分関数が偶関数や奇関数だったりした場合にはそれを利用して積分計算を回避しようという目論見です。

第1項の被積分関数は、

(3) (4) (5)

とおくと、

(6)

の形に書けて、かつは奇関数、及びは偶関数であるので、は1個の奇関数と2個の偶関数の積となっていることがわかります。

1個の奇関数と2個の偶関数の積は奇関数になることと、連続な奇関数であれば、

(7)

が成り立つことが利用できますので、( $7$ )式より、

(8)

となります。

( $2$ )式右辺第1項が0であることがわかったところで、

(9)

を計算します。

( $9$ )式の右辺は偶関数であることを利用して、積分区間を計算しやすい形に変形します。

(10)

次に、とおき、であることを利用すると…

(11)

さらに、半角の公式を用いて( $11$ )式を変形すると、

(12)

と計算できます。

一番計算が難しいと思われた項については計算の必要がないことがわかると、あとは高校数学の範囲内で計算できます。

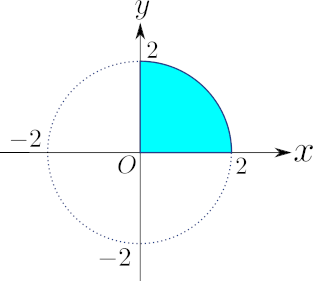
( $10$ )式が「半径2で中心角がの扇形(下図の水色の部分)の面積」を表すことがわかれば、積分計算でさえも必要ではなかったかもしれません。

ところで、”the first digits”って何桁までなのでしょうかね。

かなり気になります。

この記事は以上です。