|x|>1の場合のArctan(x)の多項式展開

はじめに

$|x|<1$のときの${\rm Arctan}x$の多項式展開の式はよく見かけるのですが、$|x|>1$の時の展開式はあまり見かける機会がありません。

そこで、計算してみることにしました。

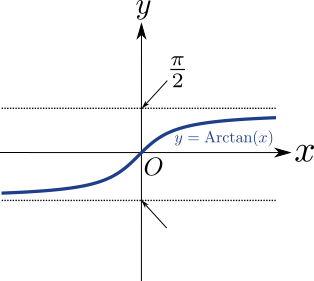
y = Arctan(x)のグラフ

Inkscape 1.3を使って$y = {\rm Arctan}(x)$のグラフを描くと…

のように描くことができます($|x| \le 5$の範囲のみ描いています)。

収束半径

なぜ$|x|>1$の時の展開式を考えるのかというと、${\rm Arctan} x$のマクローリン展開の式

\begin{align}
{\rm Arctan}\,x &= \sum_{n=0}^{\infty}\frac{(-1)^n}{2n+1}x^{2n+1}\label{eq:maclaurinseriesofarctan}
\end{align}

の右辺の式の収束半径が1なので、$|x|>1$のときには(\ref{eq:maclaurinseriesofarctan})式を直接利用することができないためです。

ここからが本題

そこで、いったん

\begin{align}
{\rm Arctan}\,x &= y \label{eq:y}
\end{align}

のように置いてみます。

(\ref{eq:y})式より、$x = \tan y$ということになるので、さらに$x = 1/u$とおいて、$u$について解いてみます。

すると、$u$は$y$を用いて、

\begin{align}
u &= \frac{1}{\tan y}\nonumber\cr
&= \tan\left( \frac{\pi}{2} – y \right)\label{eq:uy}
\end{align}

と表せるので、

\begin{align}
{\rm Arctan}\,u &= \frac{\pi}{2} – y \label{eq:yy}
\end{align}

となります。

$u=1/x$であることに留意しつつ、(\ref{eq:yy})式を$y$について解くと…

\begin{align}
y &= \frac{\pi}{2} – {\rm Arctan}\,u\nonumber\cr
&= \frac{\pi}{2} – {\rm Arctan}\left( \frac{1}{x} \right)\label{eq:finalform}
\end{align}

と解くことができます。

$|x| > 1$ならば$\displaystyle\left| \frac{1}{x} \right| < 1$なので、(\ref{eq:finalform})式の右辺第2項は(\ref{eq:maclaurinseriesofarctan})式を利用して…

\begin{align} y &= \frac{\pi}{2} - \sum_{n=0}^{\infty}\frac{(-1)^n}{2n+1}\left(\frac{1}{x}\right)^{2n+1}\nonumber\cr &= \frac{\pi}{2} - \sum_{n=0}^{\infty}\frac{(-1)^n}{2n+1}x^{-(2n+1)}\label{eq:finalexpandedform} \end{align}

と計算できます。$\blacksquare$