はじめに
人工知能(AI)や機械学習といえば超球が登場することが多いですが(※個人の感想です。)、超球の体積といえばヤコビアンということで、$n$次元の直交座標から球面座標への変数変換のためのヤコビ行列(ヤコビアン)について書きます。
$n$次元の空間の点の座標の表現方法
$n$次元空間の点$\boldsymbol{x}$の位置を$n$次元の直交座標系の座標値で表すと…
\boldsymbol{x} &= (x_1, x_2, \cdots, x_n)^{T} \label{eq:euclid}
\end{align}
$\boldsymbol{x} \in \mathbb{R}^n$と置くことができます。
一方で、同じ点を$n$次元の球面座標系の座標値で表すこともできて、
\boldsymbol{x} &= (r, \phi_1, \cdots, \phi_{n-1})^{T} \nonumber \cr
&{} \left(r \ge 0, 0 \le \phi_k \le \pi \, (1 \le k \le n-2), 0 \le \phi_{n-1} \lt 2\pi \right) \label{eq:spherical_coordinate}
\end{align}
と置くこともできます。
(\ref{eq:euclid})式の$x_1, x_2, \cdots, x_n$と(\ref{eq:spherical_coordinate})式の$r, \phi_1, \cdots, \phi_{n-1}$の間には以下の関係が成り立ちます。
\begin{pmatrix}
x_1 \cr
x_2 \cr
\vdots \cr
x_{n-1} \cr
x_n
\end{pmatrix}&= \left( \begin{array}{l}
r\sin\phi_1\sin\phi_2 \cdots \sin\phi_{n-2}\sin\phi_{n-1} \cr
r\sin\phi_1\sin\phi_2 \cdots \sin\phi_{n-2}\cos\phi_{n-1} \cr
\qquad\qquad\vdots \cr
r\sin\phi_1\cos\phi_2 \cr
r\cos\phi_1
\end{array} \right) \label{eq:euclid_spherical}
\end{align}
なお、(\ref{eq:euclid_spherical})式の右辺は、
x_k &= \begin{cases}
r \displaystyle\prod_{i=1}^{n-1}\sin\phi_i & (k = 1)\cr
r \cos\phi_{n-k+1}\displaystyle\prod_{i=1}^{n-k}\sin\phi_i & (k \gt 1) \cr
\end{cases}\label{eq:x_n}
\end{align}
とまとめることができます。
ヤコビ行列を計算します。
$\boldsymbol{x}$を$r, \phi_1, \cdots, \phi_{n-1}$の関数と考えると、(\ref{eq:euclid_spherical})式の関係よりヤコビ行列は以下のように計算できます。
\dfrac{\partial(x_1, x_2, \cdots, x_n)}{\partial(r, \phi_1, \cdots, \phi_{n-1})} &= \begin{pmatrix}
\dfrac{\partial x_1}{\partial r} & \dfrac{\partial x_1}{\partial \phi_1} & \cdots & \displaystyle\frac{\partial x_1}{\partial \phi_{n-1}} \cr
\vdots & \vdots & \ddots & \vdots \cr
\dfrac{\partial x_n}{\partial r} & \dfrac{\partial x_n}{\partial \phi_1} & \cdots & \displaystyle\frac{\partial x_n}{\partial \phi_{n-1}}
\end{pmatrix} \label{eq:jacobian_first}
\end{align}
(\ref{eq:jacobian_first})式の右辺の各成分は(\ref{eq:x_n})式を用いると以下のように表すことができます。
\dfrac{\partial x_k}{\partial r} &= \begin{cases}
\displaystyle\prod_{i=1}^{n-1}\sin\phi_i & (k = 1)\cr
\cos\phi_{n-k+1}\displaystyle\prod_{i=1}^{n-k}\sin\phi_i & (k \gt 1) \cr
\end{cases} \label{eq:diffxkr} \cr
\dfrac{\partial x_1}{\partial \phi_l} &= r \cos\phi_l\displaystyle\prod_{i=1,i \ne l}^{n-1}\sin\phi_i \label{eq:diffxonel} \cr
\dfrac{\partial x_k}{\partial \phi_l} &= \begin{cases}
r \cos\phi_{n-k+1}\cos\phi_l\displaystyle\prod_{i=1,i \ne l}^{n-k}\sin\phi_i & (x \gt 1, l \lt n-k+1) \cr
-r \displaystyle\prod_{i=1}^{n-k+1}\sin\phi_i & (x \gt 1, l = n-k+1) \cr
0 & (x \gt 1, l \gt n-k+1) \label{eq:diffxkl}
\end{cases}
\end{align}
(\ref{eq:diffxkl})式より、(\ref{eq:jacobian_first})式の右上から左下の対角線のちょっと下の成分からさらに下側のほぼ半分の個数(厳密には半分よりも少ない個数ですが)の成分が0になることがわかります。
特に、$n$列については$(3,n)$成分から$(n,n)$成分までは0になること、ならびに$\phi_{n-1}$が現れる成分は第1行及び第2行の成分に限定されることから、(\ref{eq:jacobian_first})式の右辺は(\ref{eq:diffxkr}),(\ref{eq:diffxonel})式及び(\ref{eq:diffxkl})式の結果より、(\ref{eq:jacobian_second})式の形式になっていると考えることができます。
\dfrac{\partial(x_1, x_2, \cdots, x_n)}{\partial(r, \phi_1, \cdots, \phi_{n-1})} &= \left(
\begin{array}{ccc|c}
\displaystyle\prod_{i=1}^{n-1}\sin\phi_i & r \cos\phi_1\displaystyle\prod_{i=2}^{n-1}\sin\phi_i & \cdots & r \cos\phi_{n-1}\displaystyle\prod_{i=1}^{n-2}\sin\phi_i \cr
\cos\phi_{n-1}\displaystyle\prod_{i=1}^{n-2}\sin\phi_i & r \cos\phi_{n-1}\cos\phi_1\displaystyle\prod_{i=2}^{n-2}\sin\phi_i & \cdots & -r \displaystyle\prod_{i=1}^{n-k+1}\sin\phi_i \cr \hline
\vdots & \vdots & \ddots & {\bf 0} \cr
\hline
\cos\phi_1 & -r \sin\phi_1 & \cdots & 0
\end{array}
\right) \label{eq:jacobian_second}
\end{align}
ここでいったんまとめ。
ヤコビ行列を計算すると次は変数変換に必要な行列式(ヤコビ行列式)を計算することが一般的ですが、長くなりそうなのでここでいったんひと区切りとし、次の記事あたりで続きを書きます。
この記事は以上ですが、自分もよく参照している本を紹介しますので、よろしかったらご覧いただけると幸いです。
 ちょいと野暮用で正規分布に従う独立な確率変数の和と差の確率密度関数を計算してみたので、メモ書きしてみた。
ちょいと野暮用で正規分布に従う独立な確率変数の和と差の確率密度関数を計算してみたので、メモ書きしてみた。  標準正規分布の確率密度関数をテイラー展開してから積分して累積分布関数を求めてみた。
標準正規分布の確率密度関数をテイラー展開してから積分して累積分布関数を求めてみた。  Inkscape(0.92.4)で積分経路を書いてから始める複素積分。
Inkscape(0.92.4)で積分経路を書いてから始める複素積分。 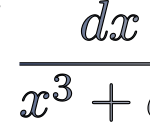 1/(x^3+a^3)の不定積分を求めてみた。
1/(x^3+a^3)の不定積分を求めてみた。