はじめに
確率変数の変数変換の方法を調べているうちに、Python3の関数で確率密度分布がVon Mises分布になる乱数を生成する関数なるものを見つけてしまい、さらにVon Mises分布の累積分布関数を計算する際に(第1種)変形Bessel関数がどこからともなく登場することがわかったので、なんでそうなるのかについての勉強も兼ねて、整数次の(第1種)変形Bessel関数からなる関数列の母関数をTaylor展開し、Von Mises分布との関係を探ることにしました。
母関数のTaylor展開
とりあえず展開。
以下この記事では、(第1種)変形Bessel関数を単に「変形Bessel関数」と書くことにします。
$k$を整数として、$k$次の変形Bessel関数の関数列$I_k(x)$の母関数$G(x;w)$は(\ref{eq:besselgenerate})式で表されます。
最初は「母関数」が「母艦数」とか変換されてしまった上にそれが辞書に学習されてしまって、なかなか変換できませんでした。困ったものです。🤔
G(x;w) &= e^{\frac{x}{2}(w+\frac{1}{w})} \label{eq:besselgenerate}
\end{align}
(\ref{eq:besselgenerate})式の右辺を$w$についてTaylor展開しますが、いきなり展開せずに、
G(x;w) &= e^{\frac{xw}{2}}\cdot e^{\frac{x}{2w}} \nonumber\cr
&= \left[ \sum_{n=0}^{\infty} \frac{1}{n!}\left(\frac{xw}{2}\right)^n\right]\left[ \sum_{m=0}^{\infty} \frac{1}{m!}\left(\frac{x}{2w}\right)^m\right] \nonumber\cr
&= \sum_{n=0}^{\infty} \sum_{m=0}^{\infty} \frac{1}{n!m!} \left(\frac{x}{2}\right)^{n+m} w^{n-m} \label{eq:firstform}
\end{align}
と展開します。
(\ref{eq:firstform})式右辺の項の総和の計算の順序(イメージ)を図にしてみました。
いったん$n=0$に固定して$m$を上図の(a)の方向に移動させて各項の値を計算してその和を求め、次に$n$を上図の(b)の方向に+1移動させてから再度上図の(a)の方向に移動させて各項の値を求める… という手順で計算を行うことを(\ref{eq:firstform})式の右辺は示しています。
ちょっと変形。
次に、(\ref{eq:firstform})式の右辺の$w$の各項の係数を調べるため、$n-m=k$とおいて(\ref{eq:firstform})式の右辺に代入し、$m$を消去します。ここで、$k$はすべての整数値をとり得ますが、$n$の値については$n$及び$n+k(=m)$が負でない整数値のみをとり得ること、すなわち$n = \max(k,0)$となることに注意が必要です。
また、$n+k$が整数の場合には$(n+k)! = \Gamma(n+k+1)$であるので、これも代入します。
すると…
G(x;w) &= \sum_{k=-\infty}^{\infty} \sum_{n=\max(k,0)}^{\infty} \frac{1}{n!\Gamma(n+k+1)} \left(\frac{x}{2}\right)^{2n+k} w^{k} \label{eq:secondform}
\end{align}
(\ref{eq:secondform})式の右辺の計算の順序(イメージ)を図にしてみました↓
まず、$k$を固定して$n$の値を上図の(a)のように移動させ、対応する各項の計算を行います。上図の$n = m+k$の直線状の格子点に対応する$(m,n)=(n-k,n)$の値に対応する項の計算を行い、その総和を計算します。次に、$k$の値を移動(増加)させると直線$n = m+k$が上図の(b)の向きに移動するので、移動した先の直線上にある格子点についても同様の計算を行うと(\ref{eq:secondform})式の右辺の値を求めることができるという寸法です。
変数の置き換え。
スポンサーリンク
(\ref{eq:secondform})式の右辺に変形Bessel関数のようなものが登場しますが、総和の計算の範囲が微妙に異なります。特に$n$の範囲が$k$の値に依存している部分についてはなんとかできないか考えます。
具体的には前節の図の白抜きの青丸の格子点(以下、この節では単に「白抜きの青丸の格子点」と書きます。)を計算の対象に含めることができれば、最初の総和の計算の範囲を$n \ge 0$の整数にできますので、ゴールに近づくことができそうです。
白抜きの青丸の格子点の$m(=n+k)$及び$n$については$m \lt 0, n \gt 0$となります。$m \lt 0$の場合には、$\displaystyle\lim_{x \to m+0}{\Gamma(x)}$及び$\displaystyle\lim_{x \to m-0}{\Gamma(x)}$は正負どちらかの$\infty$になることから、その逆数は…
\frac{1}{\Gamma(m)} &= \frac{1}{\Gamma(n+k)} \nonumber\cr
&= 0 \label{eq:gammam}
\end{align}
となります。すなわち、白抜きの青丸の格子点においては、(\ref{eq:gammamzero})式が成り立つことがわかります。
\frac{1}{n!\Gamma(n+k+1)} \left(\frac{x}{2}\right)^{2n+k} &= 0 \label{eq:gammamzero}
\end{align}
よって、$m \lt 0, n \gt 0$の場合も$n$についての総和の計算に含めても計算の結果は変わりませんので、計算の対象に追加してしまうことにします。すると、(\ref{eq:secondform})式の$n$についての総和の計算は$k$の値に関係なく行うことができて、
G(x;w) &= \sum_{k=-\infty}^{\infty} \sum_{n=0}^{\infty} \frac{1}{n!\Gamma(n+k+1)} \left(\frac{x}{2}\right)^{2n+k} w^{k}
&= \sum_{k=-\infty}^{\infty}I_k(x) w^k\label{eq:thirdform}
\end{align}
となります。
ここまでの計算で、$G(x;w)$が$k$次の変形Bessel関数の関数列$I_k(x)$の母関数であることを示すことができました。$\blacksquare$
確率分布の計算への応用
(\ref{eq:thirdform})式の$w$を$w = e^{i\theta}$と置きます。すると、(\ref{eq:thirdform})式の左辺は、
e^{\frac{x}{2}(e^{i\theta}+\frac{1}{e^{i\theta}})} &= e^{\frac{x}{2}(e^{i\theta}+e^{-i\theta})} \nonumber\cr
&= e^{x\cos\theta} \label{eq:eitheta}
\end{align}
となります。
(\ref{eq:thirdform})式の右辺は、$k$が負でない整数のときには$I_k=I_{-k}$が成り立つことから、
\sum_{k=-\infty}^{\infty}I_k(x) e^{ik\theta} &= I_0(x) + \sum_{k=1}^{\infty}I_k(x) e^{ik\theta} + \sum_{k=-\infty}^{-1}I_k(x) e^{ik\theta} \nonumber\cr
&= I_0(x) + \sum_{k=1}^{\infty}I_k(x) e^{ik\theta} + \sum_{k=1}^{\infty}I_{-k}(x) e^{-ik\theta} \nonumber\cr
&= I_0(x) + \sum_{k=1}^{\infty}I_k(x) e^{ik\theta} + \sum_{k=1}^{\infty}I_k(x) e^{-ik\theta} \nonumber\cr
&= I_0(x) + \sum_{k=1}^{\infty}I_k(x)(e^{ik\theta} + e^{-ik\theta}) \nonumber\cr
&= I_0(x) + 2\sum_{k=1}^{\infty}I_k(x)\cos k\theta \label{eq:cosktheta}
\end{align}
となります。したがって(\ref{eq:eitheta})式及び(\ref{eq:cosktheta})式をまとめると(\ref{eq:coscos})式の関係が成り立つことがわかります。
e^{x\cos\theta} &= I_0(x) + 2\sum_{k=1}^{\infty}I_k(x)\cos k\theta \label{eq:coscos}
\end{align}
また、$\theta$を$\theta – \mu$に置き換えることができて、
e^{x\cos(\theta – \mu)} &= I_0(x) + 2\sum_{k=1}^{\infty}I_k(x)\cos k(\theta – \mu) \label{eq:coscosmu}
\end{align}
が成り立つことも導けます。
(\ref{eq:coscosmu})式の右辺は、平均$\mu$のvon Mises分布(確率変数は$\theta$になります。)
p(\theta | \mu, x) &= \frac{e^{x\cos(\theta – \mu)}}{2\pi I_0(x)} \label{eq:vonMises}
\end{align}
の分子と一致しますので、(\ref{eq:vonMises})式は(\ref{eq:vonMisessecond})式のように書くこともできます。
p(\theta | \mu, x) &= \frac{1}{2\pi}\left[ 1 + 2\sum_{k=1}^{\infty}\frac{I_k(x)}{I_0(k)}\cos k(\theta – \mu) \right] \label{eq:vonMisessecond}
\end{align}
(\ref{eq:vonMisessecond})式は不定積分が計算できて、積分定数以外の項については(\ref{eq:vonMisesint})式のように計算できます。
P(\theta | \mu, x) &= \frac{1}{2\pi}\left[ \theta + 2\sum_{k=1}^{\infty}\frac{I_k(x)}{I_0(k)}\frac{\sin k(\theta – \mu)}{k} \right] \label{eq:vonMisesint}
\end{align}
まとめ
(\ref{eq:secondform})式から(\ref{eq:thirdform})式への議論については回りくどいものになっている可能性がありますが、本Webサイトの管理人たるpandaが理解したところをそのまま書いてみました。
Von Mises分布とVon Mises-Fisher分布についてはいまいち理解できていないので、理解できたところでまた書きます。
この記事は以上です。
 ちょいと野暮用で正規分布に従う独立な確率変数の和と差の確率密度関数を計算してみたので、メモ書きしてみた。
ちょいと野暮用で正規分布に従う独立な確率変数の和と差の確率密度関数を計算してみたので、メモ書きしてみた。  標準正規分布の確率密度関数をテイラー展開してから積分して累積分布関数を求めてみた。
標準正規分布の確率密度関数をテイラー展開してから積分して累積分布関数を求めてみた。 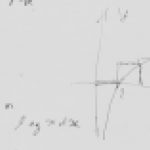 \sqrt[n]{n!}及び\sqrt[n]{n!!}がn→∞のときに∞に発散することの証明。
\sqrt[n]{n!}及び\sqrt[n]{n!!}がn→∞のときに∞に発散することの証明。  標準正規分布に従う2個の確率変数の積が従う確率密度関数を計算してみた。
標準正規分布に従う2個の確率変数の積が従う確率密度関数を計算してみた。